Page 2 sur 3 •  1, 2, 3
1, 2, 3 
 1, 2, 3
1, 2, 3 
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:45
V - Réponses aux sceptiques
Introduction
Non seulement je ne crains pas les critiques des "sceptiques", mais je les recherche au contraire. Soit le cas étudié en ressort renforcé, soit il s'avère peu solide, voire totalement expliqué (canular ou méprise), et il faut avoir l' honnêteté de le reconnaitre.
J'ai donc soumis le cas Chauvet aux virulents Sceptiques du Québec, sur le forum éponyme. Etant donné le nombre et la netteté des photos de "l'engin" (excluant a priori la méprise), ceux-ci ont attaqué bille en tête sur l'hypothèse du canular, de type "frisbee". Ils ont également remarqué une anomalie concernant le nuage de la photo N°3.
De plus la parution des quatre premiers chapitres de mon dossier sur le web a généré plusieurs courriers, généralement de félicitations, mais aussi un plus sceptique, tenant opiniâtre d'une méprise avec un ballon.
D'autre part, une personne de mon entourage, scientifique à Orsay, a rapidement proposé l'explication par un trucage photographique (photomontage), tout en prônant la thèse qu'André Frégnale avait le profil psychologique adéquat pour monter un canular.
J'ai étudié attentivement chacune de ces hypothèses , et je pense être en mesure de les réfuter toutes, de manière factuelle et objective. Tel est l'objet du présent chapitre V. Le cas Chauvet en ressort donc pour moi encore renforcé.
Anecdotiquement, j'ai remarqué à cette occasion, que tous les sceptiques sont tous immédiatement certains qu'il ne s'agit pas d'un "vrai" ovni ... mais tous pour des raisons différentes et incompatibles entre elles ! Et pour chacun d'eux, il apparait comme "évident" que son explication (généralement imaginé très vite, et en n'ayant qu'une connaissance superficielle du dossier), est la seule bonne. Or, par définition, TOUTES ces explications sauf au plus une (si j'ai tort) sont FAUSSES. Cela ne peut que nous amener à relativiser la confiance que nous pouvons mettre dans nos "certitudes", nos "premières impressions", et notre "bon sens". Seule à mon avis une étude approfondie, méthodique et objective des faits du dossier, ainsi que la recherche tenace d'éléments nouveaux et authentiques, peut permettre d'avancer utilement dans ce genre d'affaires.
Dernière minute (mars 2004): J'ai pu rentrer en contact avec Laurent Guérin, le fils de Pierre Guérin. Grâce à lui j'ai pu apprendre des détails inédits sur l'analyse que son père avait faite de ces photos, et à laquelle il a activement participé (l'article du JSE lui en donne d'ailleurs crédit). J'ai pu également corriger quelques petites inexactitudes dans mes quatre premiers chapitres. J'ai également pu avoir accès à des copies agrandies de seconde génération des photos originales, de bien meilleure qualité évidemment que les médiocres reproductions publiées dans l'encart photo du livre de Pierre Guérin. Enfin, Laurent Guérin s'est remis aux calculs de trigonométrie, et planche à nouveau en ce moment sur l'estimation des coordonnées sphériques de l'objet. J'espère pouvoir publier bientôt ses résultats. Pour tout cela, qu'il en soit ici chaleureusement remercié.
Retour au Sommaire
Le canular de type projectile/frisbee
A quelle distance se trouvait l'objet / Quelle était sa taille ?
angle en fonction de la focale et de la taille de l'image Pierre Guérin estime que l'objet se trouve à au moins 60 mètres de l'observateur grâce à un "calcul élémentaire" de profondeur de champ qu'il ne donne hélas pas. De là il en déduit la taille minimum de l'objet : 1 mètre, en raison de sa dimension angulaire mesurée sur le film (environ 1°), ce qui on en conviendra rend immédiatement peu plausible l'hypothèse du canular de type "projectile lancé en l'air" (voir mon chapitre II).
Les sceptiques ont immédiatement mis en doute ce calcul, arguant même que "En plein soleil, et avec un grand angulaire, virtuellement TOUT est net sur la photo", sous entendu : la distance minimale à laquelle l'objet se trouvait pourrait être quasiment nulle.
Laissons de coté la mauvaise foi évidente d'une telle assertion (une focale de 45 mm n'est pas un grand angulaire mais correspond au contraire exactement à la focale dite "naturelle", c'est à dire qu'elle donne à peu près le même champ de vision que celui de l'oeil humain).
Laissons aussi de coté le fait que même si cela était vrai, cela ne changerait quasiment rien à la démonstration :
* L'objet aurait pu être plus près (mettons 20 m) et donc plus petit, mais cela ne prouve pas qu'il l'était effectivement
* Le lancer et les conditions de prise de vue, pour aligner la bande noire dans le sens de la trajectoire, et donner une apparence de vol rectiligne uniforme, restaient impossible (voir le chapitre II).
Il n'en reste pas moins qu'il semble nécessaire de vérifier ce chiffre de 60 m. M. Guérin étant hélas décédé, et ses notes de travail perdues, il va donc falloir réfléchir un peu.
Rappel : l'objectif était à l'évidence réglé sur l'infini (nuage net), et l'objet lui même est très net aussi (hormis le flou de bougé des photos N°1 et 2, du à l'opérateur uniquement).
La distance minimale à partir de laquelle tout est net, jusqu'à l'infini se déduit de l'hyperfocale (h). Il n'existe pas de formule 100% exacte permettant de calculer h, notamment parce que la notion de "netteté" est éminemment variable et subjective.
Néanmoins dans la plupart des cas (hors macro), la formule suivante est acceptée : h = F²/(f * c), où :
- F est la focale de l'objectif,
- f est l'ouverture du diaphragme, et
- c est le "cercle de confusion".
NB : f est un nombre sans dimension, appelé aussi "f-stop" en anglais, et vaut le rapport entre la focale et le diamètre du diaphragme. En posant D = ouverture du diaphragme (en mm), il vient donc : h = F*D/c, autre variante connue de la formule de calcul de h.
Pour les perfectionnistes, voici un calcul complet de h, faisant appel à la bonne vieille formule de Newton (m.m' = f²). Grand merci à Laurent Guérin pour cette page !
Le terme "c" désigne justement la plus grande dimension au-delà de laquelle un point ne serait pas "net" sur le film, mais serait en fait une petite tâche. Les valeurs usuelles de c pour un film 24x36 standard vont de 0,025 mm à 0,033 mm, mais il est admis de baisser cette valeur à 20 microns voire moins pour des films de haute qualité à grain fin. Or le film utilisé par M. Frégnale (un Kodak Panatomic-X) est un film à grain fin. Prenons donc c = 0,020 mm à titre conservatoire.
La focale de l'objectif est connue et vaut 45 mm.
L'ouverture est connue aussi : f5,6. Mais il existe là une petite imprécision. En effet Guérin stipule également que l'ouverture a été augmentée d'un cran après la photo N°1. Ce qui signifierait une valeur de f=4.
Donc :
en prenant c = 0,020 mm et f = 5,6, on obtient h = 18,1 m
en prenant c = 0,020 mm et f = 4, on obtient h = 25,31 m
Ce calcul reste encore imprécis, notamment sur le facteur c. Mais d'ores et déjà on constate que l'ordre de grandeur ainsi trouvé est environ trois fois plus petit que celui calculé par Guérin (60 mètres).
Certes cela correspondrait à un frisbee "géant" de 30 à 40 cm de diamètre, qui ne doit déjà pas être commode à lancer aussi loin et aussi haut.
Mais connaissant la compétence et l'honnêteté de Pierre Guérin, un tel écart me semblait impossible. Faute d'avoir trouvé secours auprès des scientifiques et opticiens que j'ai consultés, je me suis donc mis à me documenter plus avant sur la notion de "netteté" et de profondeur de champ en photographie.
Le facteur clé est justement ce "Cercle de Confusion" (c). Or il s'avère qu'il n'existe aucune définition totalement objective impartiale et universelle de ce facteur, qui fait appel dans sa définition à la notion de "netteté", concept éminemment subjectif s'il en est !
Les valeurs "usuelles" utilisées habituellement par les photographes, même professionnels, et dont j'ai donné la fourchette ci-dessus, ne sont que des valeurs moyennes empiriques, généralement tirées d'abaques ou de calculateurs issus des fabricants (Canon, Nikon, etc.).
En fouillant un peu plus on tombe bien sur des formules, du type :
c = d/1300 (valeur moyenne pour un 35mm), ou c = d/1730 (standard Zeiss Icon), ou d est la diagonale d'une vue exprimée en millimètres. Pour un film 35 mm, dont les cotés font 24 et 36 mm, cela donne une valeur moyenne de 25 à 33 microns.
Mais encore une fois ce ne sont que des "recettes de cuisine".
C'est sur le web américain que j'ai enfin trouvé la réponse, et notamment ici pour des explications :
Et ici, j'ai trouvé enfin uen méthode de calcul, certes assez compliquée (accrochez vous en la lisant), mais rationnelle et objective. En la lisant et en la mettant en pratique, j'ai compris quel était le "paramètre manquant" dans mes premiers calculs, basés sur des valeurs empiriques usuelles de c : le facteur d'agrandissement.
En effet, plus vous pouvez agrandir - sans perte de qualité - une image, plus vous pouvez évaluer finement la netteté de chaque plan, et trouver finalement "pas net" des détails qui paraissaient nets sur un tirage de format standard.
Autrement dit plus vous pouvez réduire la valeur du cercle de confusion. La limite inférieure étant bien entendu la taille d'un grain élémentaire de l'émulsion chimique qui recouvre le film, comme le confirme cette source : "If you want it to look sharp through a 10 x loupe, or in a big enlargement, then the max COF is what your film can resolve."
Or Pierre Guérin l'a écrit, il a justement effectué des agrandissements poussés du négatif, allant jusqu'à la limite de résolution de l'émulsion utilisée.
Il a même constaté qu'à cette échelle l'étalement du bord du disque sur la photo N°3 était toujours inférieur ou égal à 10 microns, soit "sensiblement la résolution maximale du film", preuve que la mise au point était parfaite.
Il est donc hautement probable que Pierre Guérin a retenu comme valeur de c la valeur limite, c'est à dire la fameuse résolution maximale du film Panatomic-X. Elle m'est inconnue avec précision, mais elle est inférieure ou égale à 10 microns, d'après ce qui précède. Prenons donc cette valeur pratique, comme base. Cela donne immédiatement :
- pour f = 5,6, h = 36,2 m
- pour f = 4, h = 50,63 m
Introduction
Non seulement je ne crains pas les critiques des "sceptiques", mais je les recherche au contraire. Soit le cas étudié en ressort renforcé, soit il s'avère peu solide, voire totalement expliqué (canular ou méprise), et il faut avoir l' honnêteté de le reconnaitre.
J'ai donc soumis le cas Chauvet aux virulents Sceptiques du Québec, sur le forum éponyme. Etant donné le nombre et la netteté des photos de "l'engin" (excluant a priori la méprise), ceux-ci ont attaqué bille en tête sur l'hypothèse du canular, de type "frisbee". Ils ont également remarqué une anomalie concernant le nuage de la photo N°3.
De plus la parution des quatre premiers chapitres de mon dossier sur le web a généré plusieurs courriers, généralement de félicitations, mais aussi un plus sceptique, tenant opiniâtre d'une méprise avec un ballon.
D'autre part, une personne de mon entourage, scientifique à Orsay, a rapidement proposé l'explication par un trucage photographique (photomontage), tout en prônant la thèse qu'André Frégnale avait le profil psychologique adéquat pour monter un canular.
J'ai étudié attentivement chacune de ces hypothèses , et je pense être en mesure de les réfuter toutes, de manière factuelle et objective. Tel est l'objet du présent chapitre V. Le cas Chauvet en ressort donc pour moi encore renforcé.
Anecdotiquement, j'ai remarqué à cette occasion, que tous les sceptiques sont tous immédiatement certains qu'il ne s'agit pas d'un "vrai" ovni ... mais tous pour des raisons différentes et incompatibles entre elles ! Et pour chacun d'eux, il apparait comme "évident" que son explication (généralement imaginé très vite, et en n'ayant qu'une connaissance superficielle du dossier), est la seule bonne. Or, par définition, TOUTES ces explications sauf au plus une (si j'ai tort) sont FAUSSES. Cela ne peut que nous amener à relativiser la confiance que nous pouvons mettre dans nos "certitudes", nos "premières impressions", et notre "bon sens". Seule à mon avis une étude approfondie, méthodique et objective des faits du dossier, ainsi que la recherche tenace d'éléments nouveaux et authentiques, peut permettre d'avancer utilement dans ce genre d'affaires.
Dernière minute (mars 2004): J'ai pu rentrer en contact avec Laurent Guérin, le fils de Pierre Guérin. Grâce à lui j'ai pu apprendre des détails inédits sur l'analyse que son père avait faite de ces photos, et à laquelle il a activement participé (l'article du JSE lui en donne d'ailleurs crédit). J'ai pu également corriger quelques petites inexactitudes dans mes quatre premiers chapitres. J'ai également pu avoir accès à des copies agrandies de seconde génération des photos originales, de bien meilleure qualité évidemment que les médiocres reproductions publiées dans l'encart photo du livre de Pierre Guérin. Enfin, Laurent Guérin s'est remis aux calculs de trigonométrie, et planche à nouveau en ce moment sur l'estimation des coordonnées sphériques de l'objet. J'espère pouvoir publier bientôt ses résultats. Pour tout cela, qu'il en soit ici chaleureusement remercié.
Retour au Sommaire
Le canular de type projectile/frisbee
A quelle distance se trouvait l'objet / Quelle était sa taille ?
angle en fonction de la focale et de la taille de l'image Pierre Guérin estime que l'objet se trouve à au moins 60 mètres de l'observateur grâce à un "calcul élémentaire" de profondeur de champ qu'il ne donne hélas pas. De là il en déduit la taille minimum de l'objet : 1 mètre, en raison de sa dimension angulaire mesurée sur le film (environ 1°), ce qui on en conviendra rend immédiatement peu plausible l'hypothèse du canular de type "projectile lancé en l'air" (voir mon chapitre II).
Les sceptiques ont immédiatement mis en doute ce calcul, arguant même que "En plein soleil, et avec un grand angulaire, virtuellement TOUT est net sur la photo", sous entendu : la distance minimale à laquelle l'objet se trouvait pourrait être quasiment nulle.
Laissons de coté la mauvaise foi évidente d'une telle assertion (une focale de 45 mm n'est pas un grand angulaire mais correspond au contraire exactement à la focale dite "naturelle", c'est à dire qu'elle donne à peu près le même champ de vision que celui de l'oeil humain).
Laissons aussi de coté le fait que même si cela était vrai, cela ne changerait quasiment rien à la démonstration :
* L'objet aurait pu être plus près (mettons 20 m) et donc plus petit, mais cela ne prouve pas qu'il l'était effectivement
* Le lancer et les conditions de prise de vue, pour aligner la bande noire dans le sens de la trajectoire, et donner une apparence de vol rectiligne uniforme, restaient impossible (voir le chapitre II).
Il n'en reste pas moins qu'il semble nécessaire de vérifier ce chiffre de 60 m. M. Guérin étant hélas décédé, et ses notes de travail perdues, il va donc falloir réfléchir un peu.
Rappel : l'objectif était à l'évidence réglé sur l'infini (nuage net), et l'objet lui même est très net aussi (hormis le flou de bougé des photos N°1 et 2, du à l'opérateur uniquement).
La distance minimale à partir de laquelle tout est net, jusqu'à l'infini se déduit de l'hyperfocale (h). Il n'existe pas de formule 100% exacte permettant de calculer h, notamment parce que la notion de "netteté" est éminemment variable et subjective.
Néanmoins dans la plupart des cas (hors macro), la formule suivante est acceptée : h = F²/(f * c), où :
- F est la focale de l'objectif,
- f est l'ouverture du diaphragme, et
- c est le "cercle de confusion".
NB : f est un nombre sans dimension, appelé aussi "f-stop" en anglais, et vaut le rapport entre la focale et le diamètre du diaphragme. En posant D = ouverture du diaphragme (en mm), il vient donc : h = F*D/c, autre variante connue de la formule de calcul de h.
Pour les perfectionnistes, voici un calcul complet de h, faisant appel à la bonne vieille formule de Newton (m.m' = f²). Grand merci à Laurent Guérin pour cette page !
Le terme "c" désigne justement la plus grande dimension au-delà de laquelle un point ne serait pas "net" sur le film, mais serait en fait une petite tâche. Les valeurs usuelles de c pour un film 24x36 standard vont de 0,025 mm à 0,033 mm, mais il est admis de baisser cette valeur à 20 microns voire moins pour des films de haute qualité à grain fin. Or le film utilisé par M. Frégnale (un Kodak Panatomic-X) est un film à grain fin. Prenons donc c = 0,020 mm à titre conservatoire.
La focale de l'objectif est connue et vaut 45 mm.
L'ouverture est connue aussi : f5,6. Mais il existe là une petite imprécision. En effet Guérin stipule également que l'ouverture a été augmentée d'un cran après la photo N°1. Ce qui signifierait une valeur de f=4.
Donc :
en prenant c = 0,020 mm et f = 5,6, on obtient h = 18,1 m
en prenant c = 0,020 mm et f = 4, on obtient h = 25,31 m
Ce calcul reste encore imprécis, notamment sur le facteur c. Mais d'ores et déjà on constate que l'ordre de grandeur ainsi trouvé est environ trois fois plus petit que celui calculé par Guérin (60 mètres).
Certes cela correspondrait à un frisbee "géant" de 30 à 40 cm de diamètre, qui ne doit déjà pas être commode à lancer aussi loin et aussi haut.
Mais connaissant la compétence et l'honnêteté de Pierre Guérin, un tel écart me semblait impossible. Faute d'avoir trouvé secours auprès des scientifiques et opticiens que j'ai consultés, je me suis donc mis à me documenter plus avant sur la notion de "netteté" et de profondeur de champ en photographie.
Le facteur clé est justement ce "Cercle de Confusion" (c). Or il s'avère qu'il n'existe aucune définition totalement objective impartiale et universelle de ce facteur, qui fait appel dans sa définition à la notion de "netteté", concept éminemment subjectif s'il en est !
Les valeurs "usuelles" utilisées habituellement par les photographes, même professionnels, et dont j'ai donné la fourchette ci-dessus, ne sont que des valeurs moyennes empiriques, généralement tirées d'abaques ou de calculateurs issus des fabricants (Canon, Nikon, etc.).
En fouillant un peu plus on tombe bien sur des formules, du type :
c = d/1300 (valeur moyenne pour un 35mm), ou c = d/1730 (standard Zeiss Icon), ou d est la diagonale d'une vue exprimée en millimètres. Pour un film 35 mm, dont les cotés font 24 et 36 mm, cela donne une valeur moyenne de 25 à 33 microns.
Mais encore une fois ce ne sont que des "recettes de cuisine".
C'est sur le web américain que j'ai enfin trouvé la réponse, et notamment ici pour des explications :
Et ici, j'ai trouvé enfin uen méthode de calcul, certes assez compliquée (accrochez vous en la lisant), mais rationnelle et objective. En la lisant et en la mettant en pratique, j'ai compris quel était le "paramètre manquant" dans mes premiers calculs, basés sur des valeurs empiriques usuelles de c : le facteur d'agrandissement.
En effet, plus vous pouvez agrandir - sans perte de qualité - une image, plus vous pouvez évaluer finement la netteté de chaque plan, et trouver finalement "pas net" des détails qui paraissaient nets sur un tirage de format standard.
Autrement dit plus vous pouvez réduire la valeur du cercle de confusion. La limite inférieure étant bien entendu la taille d'un grain élémentaire de l'émulsion chimique qui recouvre le film, comme le confirme cette source : "If you want it to look sharp through a 10 x loupe, or in a big enlargement, then the max COF is what your film can resolve."
Or Pierre Guérin l'a écrit, il a justement effectué des agrandissements poussés du négatif, allant jusqu'à la limite de résolution de l'émulsion utilisée.
Il a même constaté qu'à cette échelle l'étalement du bord du disque sur la photo N°3 était toujours inférieur ou égal à 10 microns, soit "sensiblement la résolution maximale du film", preuve que la mise au point était parfaite.
Il est donc hautement probable que Pierre Guérin a retenu comme valeur de c la valeur limite, c'est à dire la fameuse résolution maximale du film Panatomic-X. Elle m'est inconnue avec précision, mais elle est inférieure ou égale à 10 microns, d'après ce qui précède. Prenons donc cette valeur pratique, comme base. Cela donne immédiatement :
- pour f = 5,6, h = 36,2 m
- pour f = 4, h = 50,63 m
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:46
Cette fois-ci on y est presque. L'objet était sûrement à plus de 50 mètres, et probablement au moins à 60 mètres comme l'affirme Pierre Guérin, en prenant c = 8,5 microns au lieu des 10 microns "pessimistes".
Retour au Sommaire
Calculs liés à la vitesse de l'objet
La vitesse réelle d'obturation était de 1/200 ème de seconde (Voir chapitre III), et l'objet est parfaitement net, hormis un flou de bougé de l'opérateur sur la seconde photo. Cela signifie donc qu'il ne s'est pas "beaucoup" déplacé pendant ce laps de temps, moins en tous cas que le fameux cercle de confusion (c), sinon le bord serait flou.
Or l'angle W balayé par l'image sur la pellicule, est le même que celui balayé par l'objet dans le ciel.
Posons : F=focale appareil ; y= demi-distance balayée par l'image ; Y=demi-distance balayée par l'objet ; D=Distance de l'objet à l'appareil photo.
Il vient alors : sin(W/2) = ymini / F = Y / D, d'où : Y = ymini * D / F
L'objet n'a donc pu parcourir au maximum que 2Y mètres pendant ces 1/200ème de seconde. On en déduit donc sa vitesse maximum : Vmax = 2Y * 200 (en m/s) = 2Y * 200 * 3,6 (en km/h).
Or F=45 mm, et en prenant la valeur c=0,020 mm, on a ymini=c/2=0,010mm. D'où :
* si D= 20 m, alors Vmax = 6,4 km/h
* si D = 30 m, alors Vmax = 9,4 km/h
* si D = 60 m, alors Vmax = 18,4 km/h
Or un projectile de type frisbee lancé en l'air doit avoir une vitesse élevée pour maintenir son assiette et sa trajectoire. Je ne connais pas encore cette vitesse, mais elle est à l'évidence nettement supérieure à 18 km/h. En effet un être humain court, sans se forcer, à 18 km/h. Or essayez donc de rattraper en courant, même aussi vite que vous pouvez, un frisbee lancé par l'un de vos amis ... bon courage !
Les études scientifiques que j'ai découvert sur la physique du vol du frisbee (il y en a !) prennent comme hypothèse pour des essais en soufflerie, des vitesses de 15 à 50, voire 70 m/s. Soit une vitesse minimale de 54 km/h.
D'autre part si le photographe avait suivi le mouvement du frisbee avec son appareil, pour que son image soit nette, c'est alors le reste du paysage et du décor qui auraient été flous, ce qui n'est pas le cas.
Conclusion, l'objet se trouvait à plus de 60 mètres de l'appareil photo. Il faisait donc bien au moins un mètre de diamètre, ce qui exclut tout trucage à base de projectile lancé.
Retour au Sommaire
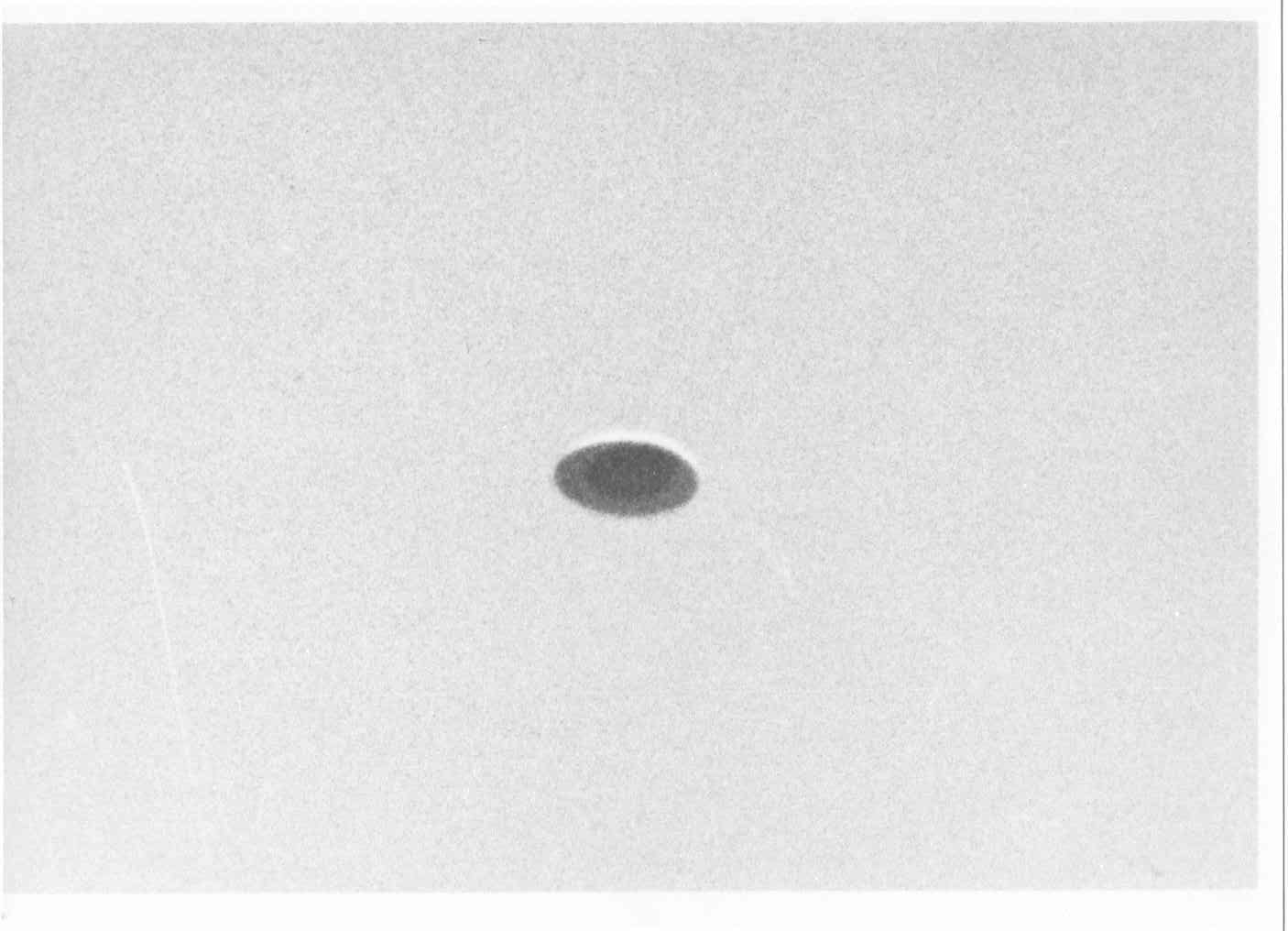
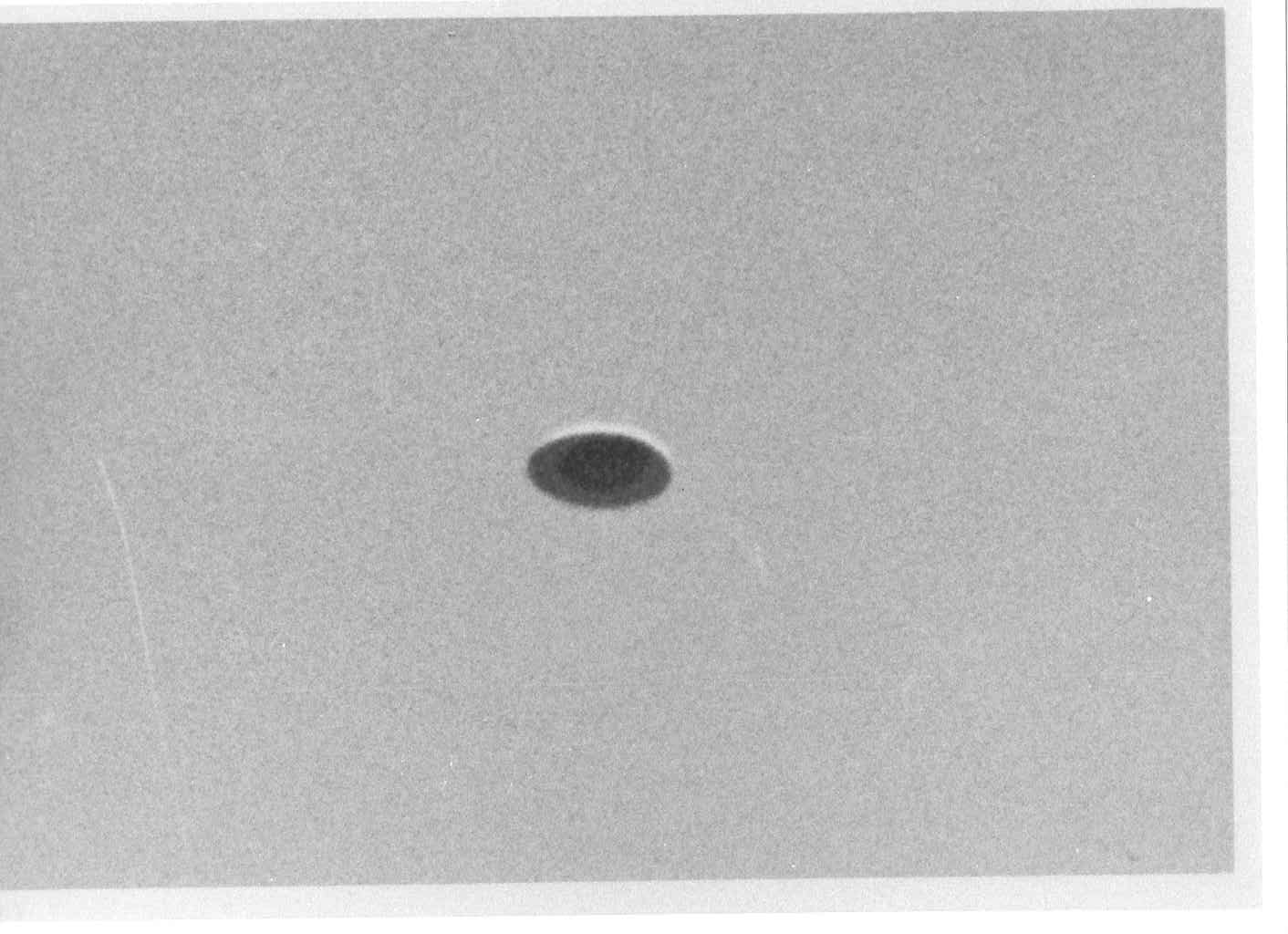
La tâche sombre sous l'objet est-elle une ombre ?
Il est évident que si la tâche sombre sous l'objet est une superstructure (saillante ou pas), ou même seulement une partie de couleur différente, alors cela rend quasiment impossible l'hypothèse d'un canular à base d'un projectile type frisbee (voir au chapitre II pourquoi). C'est probablement pourquoi, inconsciemment ou pas, les sceptiques à qui j'ai soumis ce cas ont tous immédiatement prétendu que cette "tâche" était en fait une ombre, causée par le soleil qui éclairait l'objet par l'arrière comme le prouve l'éclat brillant ("metallique") clairement visible sur le pourtour de l'objet, coté Ouest. De ce fait ils expliquaient astucieusement que cette "tâche" soit toujours orientée dans le sens de la trajectoire, puisque cette dernière était justement orientée Ouest-Est.
Hélas pour eux, cette belle idée ne tient pas la route, par construction même.
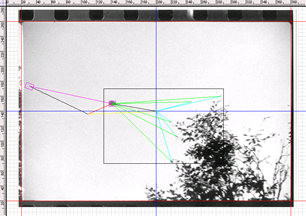
Fig 1. Simulation - Soleil au dessus au zénith : Tout le dessous du disque est dans l’ombre. Fig 2. Simulation - Soleil au dessus à 22° : Tout le dessous du disque est dans l’ombre. Le bord droit est brillant
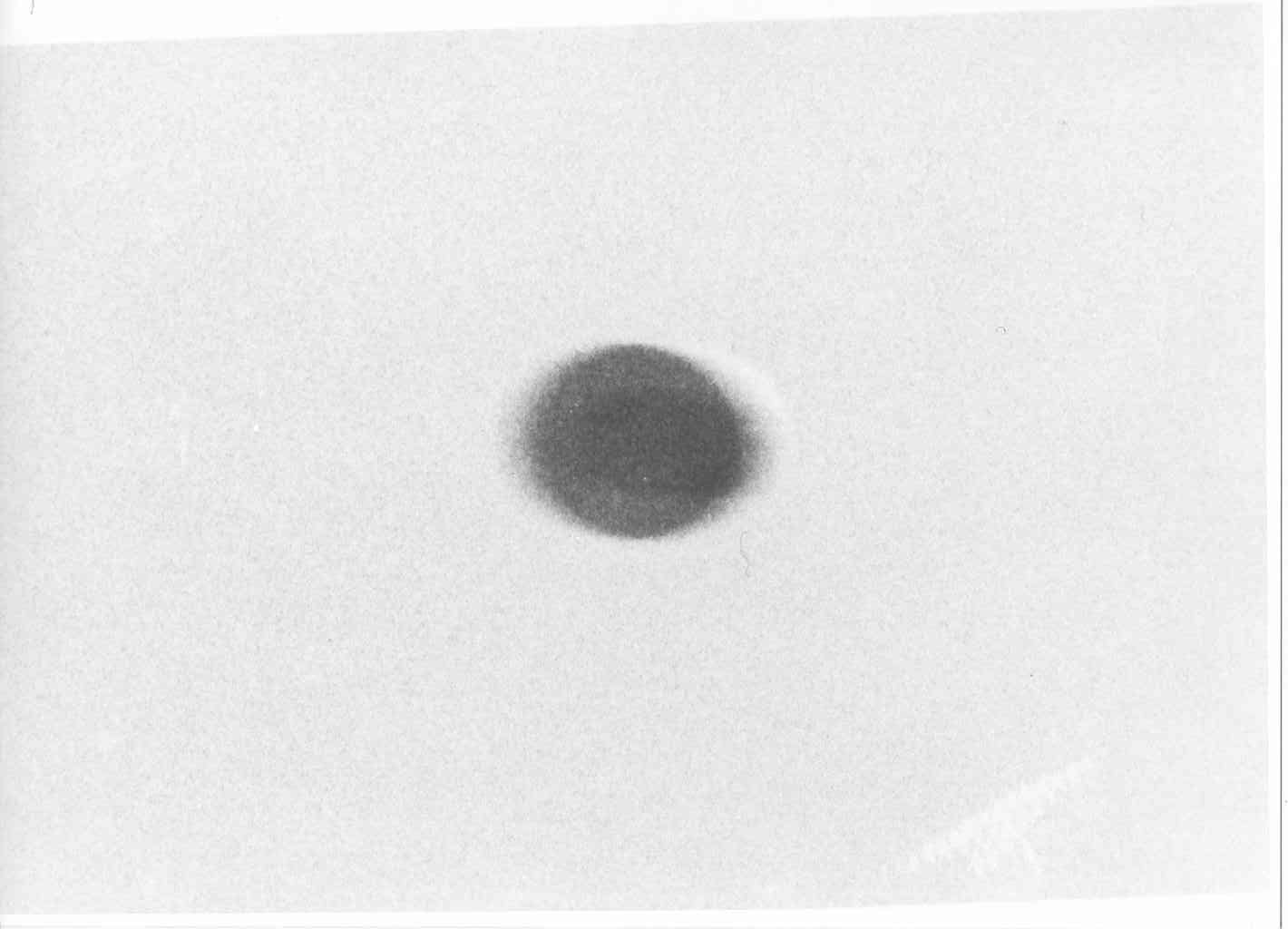
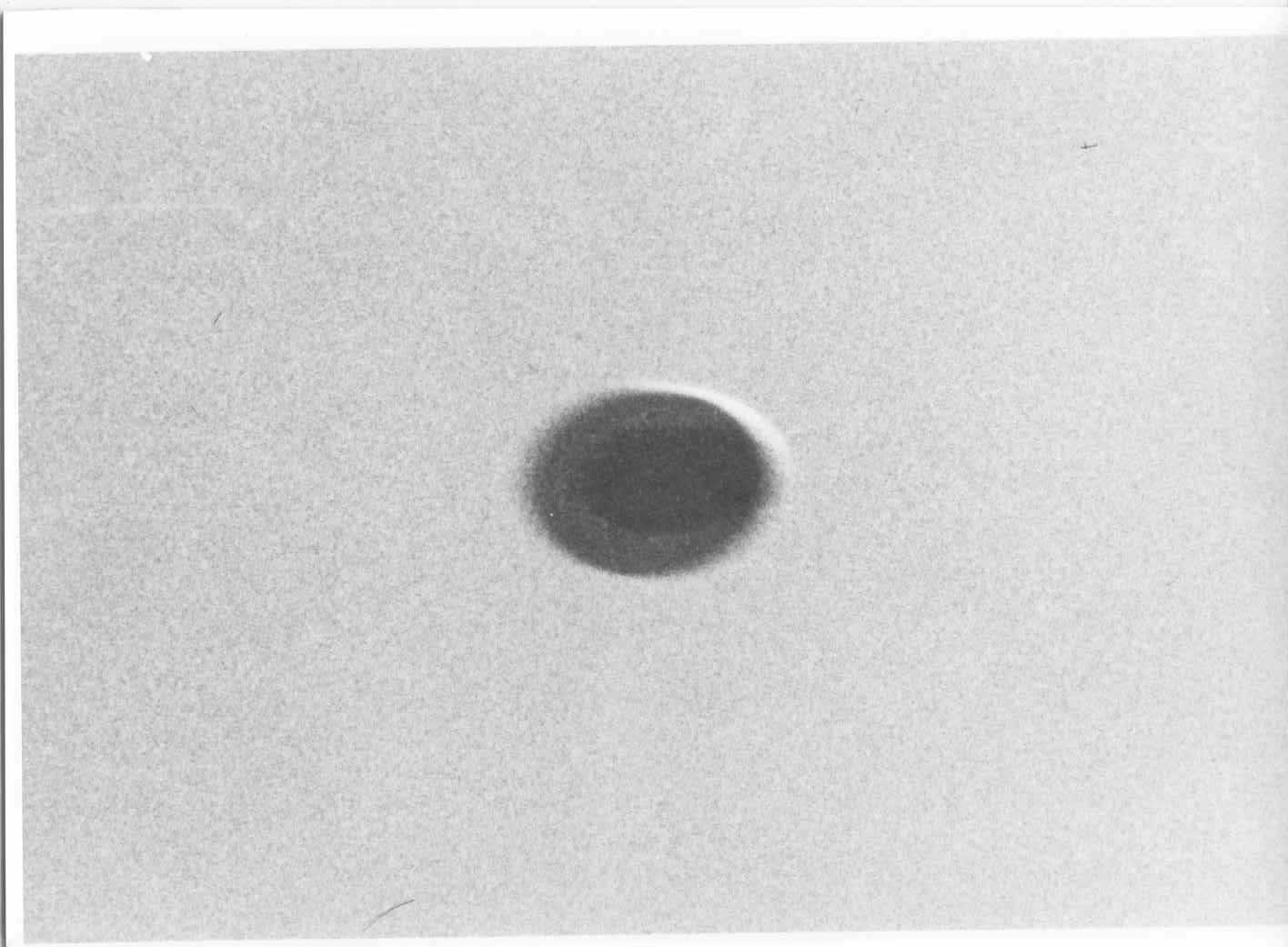
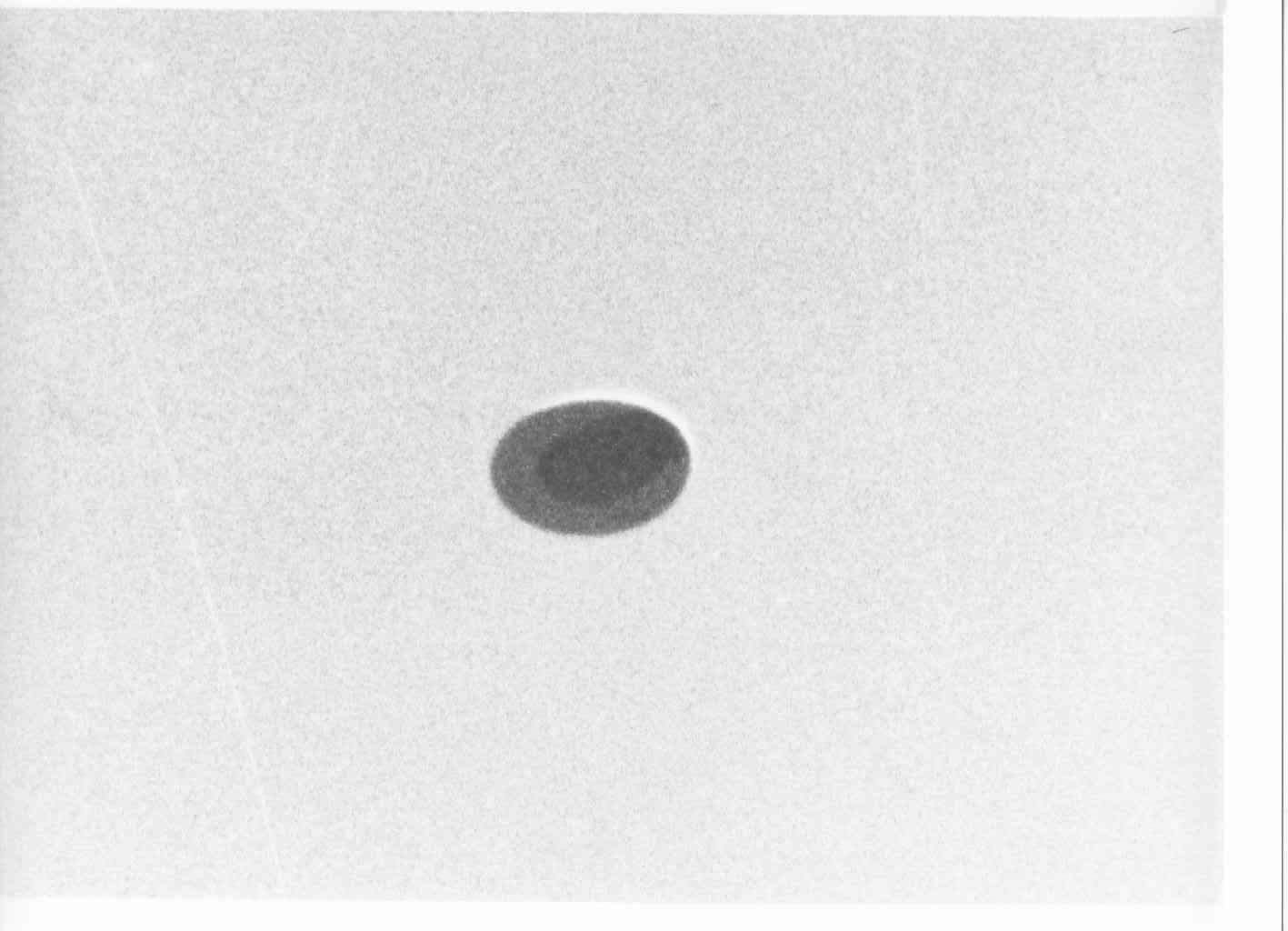
Fig 3. Simulation - Soleil au dessous et en angle rasant (situation impossible) : Le dessous du disque est éclairé. Une ombre en forme de croissant concave, générée par le bord droit du disque, apparaît. Fig 4. Photo réelle - Soleil au dessus à 22° : Tout le dessous du disque est dans l’ombre. Le « motif plus sombre » est en forme de bande terminée par un arc convexe.
McMinville On constate qu'avec le soleil placé au dessus (à 22°) il ne peut pas y avoir d'ombre particulière sous l'objet. Tout le dessous du disque devrait être dans l'ombre, un peu comme dans le célèbre cas "Trent/McMinville" en 1950, dont voici un agrandissement ci-contre.
Avouez que cette photo est très similaire à ma simulation de la figure 2 !
Seule une source lumineuse rasante, placée sous l'objet, et dans un cône angulaire très réduit pourrait projeter une ombre sur le coté droit du disque. Mais dans ce cas, cette ombre serait en forme de croissant, à bord concave, et non pas en forme de bande allongée terminée par un arc convexe.
Certains sceptiques ont imaginé qu'une "grande surface d'eau" (ie : le lac Chauvet) aurait pu modifier les conditions d'éclairage de manière à produire cette ombre. C'est peu probable car il aurait fallu pour cela que le lac soit au sud par rapport à l'observateur. Or le tracé du chemin touristique qui entoure ce site, passe au sud du lac. Un promeneur situé sur ce chemin voit donc le lac vers le Nord, ce que confirme les photos touristiques que j'ai trouvé (et qui illustrent mon site), puisqu'on y voit le Puy de Sancy au Nord. D'autre part si tel avait été le cas, nul doute que le témoin aurait signalé ce fait remarquable ("j'ai vu une soucoupe volante au dessus du lac Chauvet", et non "aux alentours du lac Chauvet").
De plus, il aurait fallu que l'objet se trouve dans une zone de l'espace extrèmement réduite, celle où la lumière solaire réfléchie par le lac frapperait le bord droit de l'objet sous une incidence adéquate. Et quand bien même, il est démontré plus haut que l'ombre générée n'aurait pas la forme requise.
Enfin, à titre anecdotique, et dans l'hypothèse d'un canular, il parait loufoque d'imaginer M. Frégnale (ou un complice) lancer son frisbee volontairement au-dessus du lac, d'aller le repêcher ensuite en bateau ou à la nage, et de recommencer cela des dizaines ... ou des centaines de fois, jusqu'à obtention des photos désirées.
Conclusion : la "tâche sombre" sous l'objet n'est pas une ombre mais fait partie intégrante de l'objet. Soit en tant que motif peint, soit en tant que superstructure saillante.
Retour au Sommaire
A propos du frisbee
"Les étudiants de l’université Yale (Connecticut) ont inventé le frisbee en 1947, en jouant avec des moules à tarte en aluminium. Ceux-ci provenaient de chez un pâtissier de Bridgeport, Joseph Frisbie, fournisseur régulier de l’université. En 1948, un jeune Américain démobilisé, Fred Morrisson, déposa un brevet pour un disque semblable en plastique. Il en céda plus tard la licence à la Wham-O californienne (cette société avait inventé le hula-hoop en 1958) qui, ayant entendu parler de l’origine du jeu, l’appela frisbee".
"January 13, 1957, marks the day that the Frisbee--the flying disc loved by dogs as well as people--was first produced by the Wham-O Company (now a division of Mattel). At that time, the disc was called the Pluto Platter, and it had already been around for almost a decade."
Bref, le frisbee n'a commencé à être commercialisé dans le grand public qu'en 1957, aux USA. Auparavant, l'ancêtre de ce jeu (utilisant de simples moules à tarte) n'était pratiqué que par les étudiants de l’université Yale, puis sur les plages de Californie du Sud.
Il est donc hautement improbable que quiconque en France ait jamais entendu parler du nom et du concept même de frisbee en 1952,a fortiori André Frégnale !
Les sceptiques qui invoquent aujourd'hui l'hypothèse frisbee pour expliquer le cas Chauvet, comme si cela allait de soi, oublient tout simplement que cela se passait il y a 51 ans, dans un contexte socio-culturel et technologique bien différent du nôtre.
Bien entendu il n'est pas TOTALEMENT exclu que, voulant faire "le canular du siècle", M. Frégnale ait également redécouvert seul de son coté les principes du vol stable du frisbee, et en ait fabriqué un en forme de soucoupe volante. Puis, l'ayant fait, il l'aurait immédiatement détruit, et n'aurait jamais cherché à l'exploiter. Bien entendu, personne dans son entourage ne l'aurait vu s'essayer à ces lancers
Cela ajoute simplement une invraisemblance de plus à une liste pourtant déjà longue. Tout cela dans le seul but d' essayer de coller à tout prix une explication "connue", fût-elle totalement improbable, à un phénomène inexplicable.
Conclusion : l'hypothèse "frisbee" est historiquement invraisemblable en 1952 et en France.
Retour au Sommaire
Retour au Sommaire
Calculs liés à la vitesse de l'objet
La vitesse réelle d'obturation était de 1/200 ème de seconde (Voir chapitre III), et l'objet est parfaitement net, hormis un flou de bougé de l'opérateur sur la seconde photo. Cela signifie donc qu'il ne s'est pas "beaucoup" déplacé pendant ce laps de temps, moins en tous cas que le fameux cercle de confusion (c), sinon le bord serait flou.
Or l'angle W balayé par l'image sur la pellicule, est le même que celui balayé par l'objet dans le ciel.
Posons : F=focale appareil ; y= demi-distance balayée par l'image ; Y=demi-distance balayée par l'objet ; D=Distance de l'objet à l'appareil photo.
Il vient alors : sin(W/2) = ymini / F = Y / D, d'où : Y = ymini * D / F
L'objet n'a donc pu parcourir au maximum que 2Y mètres pendant ces 1/200ème de seconde. On en déduit donc sa vitesse maximum : Vmax = 2Y * 200 (en m/s) = 2Y * 200 * 3,6 (en km/h).
Or F=45 mm, et en prenant la valeur c=0,020 mm, on a ymini=c/2=0,010mm. D'où :
* si D= 20 m, alors Vmax = 6,4 km/h
* si D = 30 m, alors Vmax = 9,4 km/h
* si D = 60 m, alors Vmax = 18,4 km/h
Or un projectile de type frisbee lancé en l'air doit avoir une vitesse élevée pour maintenir son assiette et sa trajectoire. Je ne connais pas encore cette vitesse, mais elle est à l'évidence nettement supérieure à 18 km/h. En effet un être humain court, sans se forcer, à 18 km/h. Or essayez donc de rattraper en courant, même aussi vite que vous pouvez, un frisbee lancé par l'un de vos amis ... bon courage !
Les études scientifiques que j'ai découvert sur la physique du vol du frisbee (il y en a !) prennent comme hypothèse pour des essais en soufflerie, des vitesses de 15 à 50, voire 70 m/s. Soit une vitesse minimale de 54 km/h.
D'autre part si le photographe avait suivi le mouvement du frisbee avec son appareil, pour que son image soit nette, c'est alors le reste du paysage et du décor qui auraient été flous, ce qui n'est pas le cas.
Conclusion, l'objet se trouvait à plus de 60 mètres de l'appareil photo. Il faisait donc bien au moins un mètre de diamètre, ce qui exclut tout trucage à base de projectile lancé.
Retour au Sommaire
La tâche sombre sous l'objet est-elle une ombre ?
Il est évident que si la tâche sombre sous l'objet est une superstructure (saillante ou pas), ou même seulement une partie de couleur différente, alors cela rend quasiment impossible l'hypothèse d'un canular à base d'un projectile type frisbee (voir au chapitre II pourquoi). C'est probablement pourquoi, inconsciemment ou pas, les sceptiques à qui j'ai soumis ce cas ont tous immédiatement prétendu que cette "tâche" était en fait une ombre, causée par le soleil qui éclairait l'objet par l'arrière comme le prouve l'éclat brillant ("metallique") clairement visible sur le pourtour de l'objet, coté Ouest. De ce fait ils expliquaient astucieusement que cette "tâche" soit toujours orientée dans le sens de la trajectoire, puisque cette dernière était justement orientée Ouest-Est.
Hélas pour eux, cette belle idée ne tient pas la route, par construction même.
Fig 1. Simulation - Soleil au dessus au zénith : Tout le dessous du disque est dans l’ombre. Fig 2. Simulation - Soleil au dessus à 22° : Tout le dessous du disque est dans l’ombre. Le bord droit est brillant
Fig 3. Simulation - Soleil au dessous et en angle rasant (situation impossible) : Le dessous du disque est éclairé. Une ombre en forme de croissant concave, générée par le bord droit du disque, apparaît. Fig 4. Photo réelle - Soleil au dessus à 22° : Tout le dessous du disque est dans l’ombre. Le « motif plus sombre » est en forme de bande terminée par un arc convexe.
McMinville On constate qu'avec le soleil placé au dessus (à 22°) il ne peut pas y avoir d'ombre particulière sous l'objet. Tout le dessous du disque devrait être dans l'ombre, un peu comme dans le célèbre cas "Trent/McMinville" en 1950, dont voici un agrandissement ci-contre.
Avouez que cette photo est très similaire à ma simulation de la figure 2 !
Seule une source lumineuse rasante, placée sous l'objet, et dans un cône angulaire très réduit pourrait projeter une ombre sur le coté droit du disque. Mais dans ce cas, cette ombre serait en forme de croissant, à bord concave, et non pas en forme de bande allongée terminée par un arc convexe.
Certains sceptiques ont imaginé qu'une "grande surface d'eau" (ie : le lac Chauvet) aurait pu modifier les conditions d'éclairage de manière à produire cette ombre. C'est peu probable car il aurait fallu pour cela que le lac soit au sud par rapport à l'observateur. Or le tracé du chemin touristique qui entoure ce site, passe au sud du lac. Un promeneur situé sur ce chemin voit donc le lac vers le Nord, ce que confirme les photos touristiques que j'ai trouvé (et qui illustrent mon site), puisqu'on y voit le Puy de Sancy au Nord. D'autre part si tel avait été le cas, nul doute que le témoin aurait signalé ce fait remarquable ("j'ai vu une soucoupe volante au dessus du lac Chauvet", et non "aux alentours du lac Chauvet").
De plus, il aurait fallu que l'objet se trouve dans une zone de l'espace extrèmement réduite, celle où la lumière solaire réfléchie par le lac frapperait le bord droit de l'objet sous une incidence adéquate. Et quand bien même, il est démontré plus haut que l'ombre générée n'aurait pas la forme requise.
Enfin, à titre anecdotique, et dans l'hypothèse d'un canular, il parait loufoque d'imaginer M. Frégnale (ou un complice) lancer son frisbee volontairement au-dessus du lac, d'aller le repêcher ensuite en bateau ou à la nage, et de recommencer cela des dizaines ... ou des centaines de fois, jusqu'à obtention des photos désirées.
Conclusion : la "tâche sombre" sous l'objet n'est pas une ombre mais fait partie intégrante de l'objet. Soit en tant que motif peint, soit en tant que superstructure saillante.
Retour au Sommaire
A propos du frisbee
"Les étudiants de l’université Yale (Connecticut) ont inventé le frisbee en 1947, en jouant avec des moules à tarte en aluminium. Ceux-ci provenaient de chez un pâtissier de Bridgeport, Joseph Frisbie, fournisseur régulier de l’université. En 1948, un jeune Américain démobilisé, Fred Morrisson, déposa un brevet pour un disque semblable en plastique. Il en céda plus tard la licence à la Wham-O californienne (cette société avait inventé le hula-hoop en 1958) qui, ayant entendu parler de l’origine du jeu, l’appela frisbee".
"January 13, 1957, marks the day that the Frisbee--the flying disc loved by dogs as well as people--was first produced by the Wham-O Company (now a division of Mattel). At that time, the disc was called the Pluto Platter, and it had already been around for almost a decade."
Bref, le frisbee n'a commencé à être commercialisé dans le grand public qu'en 1957, aux USA. Auparavant, l'ancêtre de ce jeu (utilisant de simples moules à tarte) n'était pratiqué que par les étudiants de l’université Yale, puis sur les plages de Californie du Sud.
Il est donc hautement improbable que quiconque en France ait jamais entendu parler du nom et du concept même de frisbee en 1952,a fortiori André Frégnale !
Les sceptiques qui invoquent aujourd'hui l'hypothèse frisbee pour expliquer le cas Chauvet, comme si cela allait de soi, oublient tout simplement que cela se passait il y a 51 ans, dans un contexte socio-culturel et technologique bien différent du nôtre.
Bien entendu il n'est pas TOTALEMENT exclu que, voulant faire "le canular du siècle", M. Frégnale ait également redécouvert seul de son coté les principes du vol stable du frisbee, et en ait fabriqué un en forme de soucoupe volante. Puis, l'ayant fait, il l'aurait immédiatement détruit, et n'aurait jamais cherché à l'exploiter. Bien entendu, personne dans son entourage ne l'aurait vu s'essayer à ces lancers
Cela ajoute simplement une invraisemblance de plus à une liste pourtant déjà longue. Tout cela dans le seul but d' essayer de coller à tout prix une explication "connue", fût-elle totalement improbable, à un phénomène inexplicable.
Conclusion : l'hypothèse "frisbee" est historiquement invraisemblable en 1952 et en France.
Retour au Sommaire
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:46
Les lanceurs de ball-trap
Afin de "crédibiliser" son hypothèse, un sceptique a même suggéré que l'objet de type frisbee avait été lancé au moyen d'une machine de type "Ball-trap". Dans son esprit, cela permettait d'assurer une plus grande vitesse et une plus grande stabilité dans la trajectoire, et expliquer ainsi sa parfaite horizontalité.
Aussi absurde que cette hypothèse puisse être il m'amuse d'en dire deux mots quand même. Ne serait-ce que pour illustrer jusqu'à quels extrèmes des sceptiques donneurs de leçons d'objectivité et de rigueur, sont prêts à aller.
Les machines de ball-trap lancent des plateaux d'argile de 11 cm de diamètre et d'environ 100 g. Imaginez les modifications à apporter sur un tel lanceur pour lui faire éjecter des plateaux de 1m de diamètre !
Les machines de ball-trap éjectent ces plateaux selon un certain angle, depuis le sol. Pour obtenir une trajectoire horizontale de l'objet il aurait fallu, non seulement modifier cet angle de départ sur la machine, mais également la hisser à plusieurs dizaines de mètres de haut (puisque l'objet, à supposer qu'il se trouve au plus près à 60 mètres de l'appareil photo, se trouve également par voie de conséquence, à près de 40 mètres de hauteur).
Les machines de ball-trap étaient rares et très coûteuses en 1952. Il est peu probable qu'un simple particulier ait pu s'offrir un tel luxe, surtout pour un simple canular.
Il est encore plus improbable que M. Frégnale ait pu s'acheter un objet aussi insolite sans déclencher la curiosité du voisnage, lui qui n'était pas tireur. Sans compter qu'il lui aurait fallu un ou deux complices pour manipuler et hisser cette machine en hauteur, ainsi que du matériel encombrant ... fort peu discret tout ça.
Retour au Sommaire
Considérations psychologiques à propos du "canular"
Les "faiblesses humaines"
Bien évidemment, l'une des premières réactions des "sceptiques" (qu'il revendiquent ce terme ou bien qu'ils s'en défendent) face à un tel cas troublant, est de mettre en cause la personnalité du témoin présumé, et de chercher a posteriori les ressorts psychologiques qui pourraient justifier le montage d'un canular aussi sophistiqué.
A titre d'illustration, voici un extrait d'un mail que l'une de mes relations, par ailleurs scientifique, m'a adressé après que je l'ai sollicité sur ce dossier :
"Manifestement d'une intelligence au dessus de la moyenne, nourrie par des dons d'observation et une inventivité remarquables, il n'a pas eu la carrière ni le statut social auxquels il pouvait légitimement aspirer. Toutes les conditions me semblent réunies pour imaginer un formidable canular à base de photos, à l'image de celui du monstre du Loch Ness, qu'il avait certainement la capacité de réaliser parfaitement, à une époque où il ne se passait pas de semaine sans que la presse fasse état d'un nouveau témoignage (j'avais 8 ans et ce souvenir m'a marqué). Sa motivation ? comme souvent en pareil cas, le sentiment de supériorité que l'on tire de la mystification de personnes éminentes, du public ou de notables, renforçant sa conviction d'être injustement méconnu par la société. Sil est vrai que les quatre photos sont sur une même bande de négatif, et encadrées par des prises de vue anodines, rien ne dit que ce soit son premier essai, ni que les photos aient été prises dans un court intervalle de temps, dans l'hypothèse d'un canular."
C'est justement pour contourner le caractère totalement subjectif de tels jugements, que je concentre la majeure partie de mes efforts sur des éléments factuels et objectifs (voir plus haut). En effet, même si nous tombions tous d'accord un jour pour admettre qu'André Frégnale avait effectivement le profil psychologique favorable pour imaginer et réaliser un tel canular (ce dont je ne suis toujours pas convaincu), cela ne prouverait nullement qu'il l'ai réellement fait, ni même qu'il ait eut simplement l'intention de le faire.
Autrement dit, en prenant une analogie judiciaire, ce n'est pas parce que M. Frégnale avait le "mobile", qu'il avait aussi la "possibilité matérielle" de le faire, ni a fortiori qu'il l'a réellement fait.
Or il me semble justement avoir avancé de nombreux arguments, faits et raisonnements factuels dans ce chapitre ainsi que dans le chapitre II, qui démontrent l'impossibilité matérielle de réaliser ce trucage. Avant d'avancer donc une explication attentant à la probité et à la sincérite d'une personne, il me parait indispensable au préalable de prouver que je me suis trompé dans mes démonstrations.
Sur le fond maintenant, l'hypothèse d'un canular me parait au contraire invraisemblable. Les renseignements que j'ai pu recueillir sur André Frégnale ne dépeignent nullement un homme aigri de ne pas être reconnu par l'élite "à sa juste valeur". Compte tenu de l'époque, et bien que n'ayant pas de diplôme supérieur, il avait un statut social respectable, et avait même enseigné dans un lycée. De plus, son coté "original" et libertaire faisait qu'il ne se serait de toutes façons pas plu dans un travail de bureau ou de labo routinier. Il était trop heureux de sa liberté, de pouvoir profiter de la nature à sa guise, sans comptes à rendre à personne. Je pense donc qu'il "n'aspirait" pas du tout à la carrière classique d'un ingénieur ou d'un chercheur.
Par ailleurs cette motivation supposée (mystifier les élites) implique par construction que son auteur la dévoile un jour ou l'autre : ce sera son jour de gloire, sa revanche. Or là rien ! Vingt ans après les faits, alors que ce cas était retombé depuis bien longtemps dans l'oubli, André Frégnale correspondait encore avec une petite association ufologique Belge (la désormais célèbre SOBEPS), en essayant de comprendre "ce que c'était". André Frégnale n'a jamais révélé (au moins publiquement) ce prétendu canular.
Or il ne risquait aucune opprobre publique de la part de ses voisins ou relations en dévoilant sa supercherie sur le tard, puisqu'il avait déménagé avec sa soeur, dès les années soixante, dans le sud de la France, loin de son Auvergne natale.
Par ailleurs Frégnale était un solitaire, cela au moins est certain. Or le montage d'un tel canular aurait nécessité au moins un complice. Quelqu'un de dévoué, en qui il puisse avoir une totale confiance, et qui garderait le secret ensuite jusqu'à la tombe. Connaissant désormais un peu mieux les Frégnale et leur mode de vie, ceci parait impossible.
Et puis, quitte à truquer, pourquoi déclarer avoir vu une soucoupe qui se "traine" lamentablement à 170 km/h, moins vite qu'un avion de l'époque, et en ligne droite ? Pourquoi ne pas avoir décrit un brusque virage à 90° et une accélération foudroyante qui aurait fait disparaitre la soucoupe de sa vue instantanément. Bref, pourquoi avoir insisté sur un comportement aussi peu étrange, alors que l'irruption des soucoupes depuis 1947 avait justement surpris les témoins, et fait la une des journaix, à cause de leurs performances en vol "impossibles" ?
Enfin, l'honnêteté et l'intégrité de Pierre Guérin lui même, qu'aucun sceptique à ce jour n'a quand même osé mettre explicitement en doute, sont encore renforcées lorsqu'on sait qu'il a, sur un cas similaire, conclu après analyse au trucage d'une photo d'un ovni soit-disant pris en Corse en 1971, et qu'il a réussi à faire avouer l'auteur de ce canular.
Arguments de mauvaise foi
Certains sceptiques ont même été jusqu'à dire que le dossier Chauvet était creux, voire douteux, car "tous les témoins sont morts, et le négatif original a disparu".
J'avoue que là j'ai du mal à me contenir. Oui, l'être humain n'est pas immortel, et 51 ans après les faits, il est normal que les principaux acteurs soient décédés.
Mais les témoins et les négatifs ont été à la disposition de la Science, des autorités, des ufologues, et des sceptiques pendant au moins 30 ans !
=> Pourquoi seul Pierre Guérin a-t-il eu le courage de briser le tabou de l'establishment scientifique en étudiant ce cas ?
=> Pourquoi, malgré un article dans Sciences et Avenir N°307 en septembre 1972, où Guérin donnait déjà l'essentiel de son analyse des clichés, personne parmi la communauté scientifique ou intellectuelle ne s'est rué sur ce cas, presque trop beau pour être vrai ?
De plus, concernant le négatif, cette remarque perfide relève d'un certain révisionnisme de mauvais goût. En effet, le négatif original a bel et bien été analysé, scientifiquement et au micrsocope, par un expert : Pierre Guérin lui même. Il me parait donc indigne de remettre en cause ainsi de manière insidieuse la probité de cet homme, en insinuant qu'il aurait pu mal interpréter les résultats, ou en omettre certains.
Afin de "crédibiliser" son hypothèse, un sceptique a même suggéré que l'objet de type frisbee avait été lancé au moyen d'une machine de type "Ball-trap". Dans son esprit, cela permettait d'assurer une plus grande vitesse et une plus grande stabilité dans la trajectoire, et expliquer ainsi sa parfaite horizontalité.
Aussi absurde que cette hypothèse puisse être il m'amuse d'en dire deux mots quand même. Ne serait-ce que pour illustrer jusqu'à quels extrèmes des sceptiques donneurs de leçons d'objectivité et de rigueur, sont prêts à aller.
Les machines de ball-trap lancent des plateaux d'argile de 11 cm de diamètre et d'environ 100 g. Imaginez les modifications à apporter sur un tel lanceur pour lui faire éjecter des plateaux de 1m de diamètre !
Les machines de ball-trap éjectent ces plateaux selon un certain angle, depuis le sol. Pour obtenir une trajectoire horizontale de l'objet il aurait fallu, non seulement modifier cet angle de départ sur la machine, mais également la hisser à plusieurs dizaines de mètres de haut (puisque l'objet, à supposer qu'il se trouve au plus près à 60 mètres de l'appareil photo, se trouve également par voie de conséquence, à près de 40 mètres de hauteur).
Les machines de ball-trap étaient rares et très coûteuses en 1952. Il est peu probable qu'un simple particulier ait pu s'offrir un tel luxe, surtout pour un simple canular.
Il est encore plus improbable que M. Frégnale ait pu s'acheter un objet aussi insolite sans déclencher la curiosité du voisnage, lui qui n'était pas tireur. Sans compter qu'il lui aurait fallu un ou deux complices pour manipuler et hisser cette machine en hauteur, ainsi que du matériel encombrant ... fort peu discret tout ça.
Retour au Sommaire
Considérations psychologiques à propos du "canular"
Les "faiblesses humaines"
Bien évidemment, l'une des premières réactions des "sceptiques" (qu'il revendiquent ce terme ou bien qu'ils s'en défendent) face à un tel cas troublant, est de mettre en cause la personnalité du témoin présumé, et de chercher a posteriori les ressorts psychologiques qui pourraient justifier le montage d'un canular aussi sophistiqué.
A titre d'illustration, voici un extrait d'un mail que l'une de mes relations, par ailleurs scientifique, m'a adressé après que je l'ai sollicité sur ce dossier :
"Manifestement d'une intelligence au dessus de la moyenne, nourrie par des dons d'observation et une inventivité remarquables, il n'a pas eu la carrière ni le statut social auxquels il pouvait légitimement aspirer. Toutes les conditions me semblent réunies pour imaginer un formidable canular à base de photos, à l'image de celui du monstre du Loch Ness, qu'il avait certainement la capacité de réaliser parfaitement, à une époque où il ne se passait pas de semaine sans que la presse fasse état d'un nouveau témoignage (j'avais 8 ans et ce souvenir m'a marqué). Sa motivation ? comme souvent en pareil cas, le sentiment de supériorité que l'on tire de la mystification de personnes éminentes, du public ou de notables, renforçant sa conviction d'être injustement méconnu par la société. Sil est vrai que les quatre photos sont sur une même bande de négatif, et encadrées par des prises de vue anodines, rien ne dit que ce soit son premier essai, ni que les photos aient été prises dans un court intervalle de temps, dans l'hypothèse d'un canular."
C'est justement pour contourner le caractère totalement subjectif de tels jugements, que je concentre la majeure partie de mes efforts sur des éléments factuels et objectifs (voir plus haut). En effet, même si nous tombions tous d'accord un jour pour admettre qu'André Frégnale avait effectivement le profil psychologique favorable pour imaginer et réaliser un tel canular (ce dont je ne suis toujours pas convaincu), cela ne prouverait nullement qu'il l'ai réellement fait, ni même qu'il ait eut simplement l'intention de le faire.
Autrement dit, en prenant une analogie judiciaire, ce n'est pas parce que M. Frégnale avait le "mobile", qu'il avait aussi la "possibilité matérielle" de le faire, ni a fortiori qu'il l'a réellement fait.
Or il me semble justement avoir avancé de nombreux arguments, faits et raisonnements factuels dans ce chapitre ainsi que dans le chapitre II, qui démontrent l'impossibilité matérielle de réaliser ce trucage. Avant d'avancer donc une explication attentant à la probité et à la sincérite d'une personne, il me parait indispensable au préalable de prouver que je me suis trompé dans mes démonstrations.
Sur le fond maintenant, l'hypothèse d'un canular me parait au contraire invraisemblable. Les renseignements que j'ai pu recueillir sur André Frégnale ne dépeignent nullement un homme aigri de ne pas être reconnu par l'élite "à sa juste valeur". Compte tenu de l'époque, et bien que n'ayant pas de diplôme supérieur, il avait un statut social respectable, et avait même enseigné dans un lycée. De plus, son coté "original" et libertaire faisait qu'il ne se serait de toutes façons pas plu dans un travail de bureau ou de labo routinier. Il était trop heureux de sa liberté, de pouvoir profiter de la nature à sa guise, sans comptes à rendre à personne. Je pense donc qu'il "n'aspirait" pas du tout à la carrière classique d'un ingénieur ou d'un chercheur.
Par ailleurs cette motivation supposée (mystifier les élites) implique par construction que son auteur la dévoile un jour ou l'autre : ce sera son jour de gloire, sa revanche. Or là rien ! Vingt ans après les faits, alors que ce cas était retombé depuis bien longtemps dans l'oubli, André Frégnale correspondait encore avec une petite association ufologique Belge (la désormais célèbre SOBEPS), en essayant de comprendre "ce que c'était". André Frégnale n'a jamais révélé (au moins publiquement) ce prétendu canular.
Or il ne risquait aucune opprobre publique de la part de ses voisins ou relations en dévoilant sa supercherie sur le tard, puisqu'il avait déménagé avec sa soeur, dès les années soixante, dans le sud de la France, loin de son Auvergne natale.
Par ailleurs Frégnale était un solitaire, cela au moins est certain. Or le montage d'un tel canular aurait nécessité au moins un complice. Quelqu'un de dévoué, en qui il puisse avoir une totale confiance, et qui garderait le secret ensuite jusqu'à la tombe. Connaissant désormais un peu mieux les Frégnale et leur mode de vie, ceci parait impossible.
Et puis, quitte à truquer, pourquoi déclarer avoir vu une soucoupe qui se "traine" lamentablement à 170 km/h, moins vite qu'un avion de l'époque, et en ligne droite ? Pourquoi ne pas avoir décrit un brusque virage à 90° et une accélération foudroyante qui aurait fait disparaitre la soucoupe de sa vue instantanément. Bref, pourquoi avoir insisté sur un comportement aussi peu étrange, alors que l'irruption des soucoupes depuis 1947 avait justement surpris les témoins, et fait la une des journaix, à cause de leurs performances en vol "impossibles" ?
Enfin, l'honnêteté et l'intégrité de Pierre Guérin lui même, qu'aucun sceptique à ce jour n'a quand même osé mettre explicitement en doute, sont encore renforcées lorsqu'on sait qu'il a, sur un cas similaire, conclu après analyse au trucage d'une photo d'un ovni soit-disant pris en Corse en 1971, et qu'il a réussi à faire avouer l'auteur de ce canular.
Arguments de mauvaise foi
Certains sceptiques ont même été jusqu'à dire que le dossier Chauvet était creux, voire douteux, car "tous les témoins sont morts, et le négatif original a disparu".
J'avoue que là j'ai du mal à me contenir. Oui, l'être humain n'est pas immortel, et 51 ans après les faits, il est normal que les principaux acteurs soient décédés.
Mais les témoins et les négatifs ont été à la disposition de la Science, des autorités, des ufologues, et des sceptiques pendant au moins 30 ans !
=> Pourquoi seul Pierre Guérin a-t-il eu le courage de briser le tabou de l'establishment scientifique en étudiant ce cas ?
=> Pourquoi, malgré un article dans Sciences et Avenir N°307 en septembre 1972, où Guérin donnait déjà l'essentiel de son analyse des clichés, personne parmi la communauté scientifique ou intellectuelle ne s'est rué sur ce cas, presque trop beau pour être vrai ?
De plus, concernant le négatif, cette remarque perfide relève d'un certain révisionnisme de mauvais goût. En effet, le négatif original a bel et bien été analysé, scientifiquement et au micrsocope, par un expert : Pierre Guérin lui même. Il me parait donc indigne de remettre en cause ainsi de manière insidieuse la probité de cet homme, en insinuant qu'il aurait pu mal interpréter les résultats, ou en omettre certains.
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:46
L'anomalie du nuage
Plusieurs sceptiques perspicaces ont remarqué que le nuage bas, visible sur la photo N°3, n'était plus du tout visible sur la photo N°4, ce qui paraît effectivement étrange (à première vue, on s'attendrait à en voir au moins un bout). De là à imaginer que les photos ont été prises à bien plus que 8 secondes d'intervalle ... bref, ce pourrait être un petit indice de plus en faveur du canular.
Voyons donc de quoi il retourne exactement.
Tout d'abord les 4 photos sont compatibles avec les conditions météorologiques du 18/07/1952. Les archives de la Météorologie Nationale auxquelles j'ai eu accès indiquent en effet pour ce jour là :
"Ciel clair, nébulosité = 2/10°", ce qui correspond bien à la description du témoin et aux photos : ciel uniformément bleu, avec quelques nuages bas à l'horizon (strato-cumulus, visible en photo N°4).
Sur les photos 3 et 4 l'appareil est tenu verticalement, la largeur de l'image est donc de 24 mm. Connaissant la focale on en déduit immédiatement le champ angulaire balayé par ces photos : un peu moins de 30°.
Calculons maintenant le déplacement angulaire entre les photos 3 et 4. Il se trouve que sur ces deux photos, l'objet est presque centré, et se trouve environ à 62% de largeur du cadre (ce qui est logique, André Frégnale étant un photographe quasi-pro, il a réussi à garder l'objectif pointé sur l'objet).
Donc, on peut estimer avec une très bonne approximation, que le déplacement angulaire de l'objectif, est quasiment le même que celui de l'objet. Or celui-ci se déduit très facilement des résultats de l'analyse de Pierre guérin (Cf. chapitre III) :
Db = b4 - b3
Db = 61,5° - 38° = 23,5°
Il y a donc un écart d'un peu plus de 6° (6,4 plus précisément). On devrait donc voir l'extrémité gauche du nuage de la photo N°3, sur près d'un quart de la photo N°4, en bas et à droite.
Lire au chapitre VI, l'analyse détaillée des mêmes photos par Laurent Guérin, fils de Pierre Guérin. En reprenant tous les calculs de zéro, et en tenant compte des marges d'erreur inévitables, il montre qu'il est possible de faire varier les ai et bi pour que, sans déroger au modèle mathématique de trajectoire déduit du témoignage de Frégnale, ils conduisent à une variation d'azimut suffisante pour que le nuage de la photo 3 n'apparaisse plus sur la photo 4.
La méprise avec un ballon publicitaire
A la lecture des coupures de presse que j'ai retrouvé auprès des archives de La Montagne de 1952 (voir chapitre IV), un lecteur attentif a noté l'épisode du ballon publicitaire échappé de la caravane du Tour de France le 18 juillet 1952 à l'arrivée à Vichy. Il a alors défendu avec opiniatreté l'idée que l'objet du lac Chauvet était ce ballon.
Cette hypothèse n'est pas plausible du tout.
Tout d'abord l'objet photographié n'a absolument pas l'aspect d'un ballon, a fortiori publicitaire. Ce dernier a vocation à être vu du plus grand nombre, et à rendre instantanément reconnaissable la marque dont il fait la promotion. Pour ce faire ils sont généralement très colorés et couverts d'inscriptions géantes et de logos. Or l'objet est d'une couleur uniforme (grisâtre d'après le témoin), et sans inscription.
D'autre part la trajectoire qu'aurait du suivre ce ballon parti de Vichy est totalement impossible. En effet les vents soufflaient Nord-Ouest/Sud-Est ce jour là (attesté par la météorologie nationale) à 60 km/h. Le ballon a donc du filer vers l'Est, vers St Etienne probablement.
Mon contradicteur a alors imaginé que, ayant rencontré les contreforts du massif central, le ballon les avait contourné par l'ouest, toujours en montant, pour être ensuite pris par les vents d'Ouest qui soufflaient près du lac Chauvet, et passer ainsi au-dessus d'André Frégnale (voir tracé brun sur cette carte.
Mais cela aussi est improbable. Il y a en effet un chemin bien plus naturel et plus facile pour un ballon partant de Vichy : celui de la vallée de l'Allier, puis de la Dore. Ce chemin reste à une altitude basse, et orientée Sud/Sud-Est.
Devant ces contre-arguments, mon contradicteur a généralisé son explication à "n'importe quel genre de ballon", par exemple un ballon de photographie aérienne de chantier, de provenance inconnue, et porté par le vent sur le lac Chauvet.
Et puis il s'est finalement rallié à mon opinion : seul un hasard extraordinaire (que j'ai calculé au chapitre II) aurait pu faire que la tâche sombre sous l'objet soit orientée chaque fois dans le sens de la trajectoire. Avec un objet porté par le vent (tel un ballon), cette tâche devrait logiquement avoir une position quelconque.
Retour au Sommaire
La méprise avec un objet de plage emporté par le vent
Sur la liste de discussion francom.ovni, l'ufologue sceptique Dominique Caudron a soutenu l'idée que l'objet du lac Chauvet était "évidemment" un objet de plage emporté par le vent, de type : parasol, matelas pneumatique, bateau gonflable, ballon de plage.
Cette thèse ne tient pas debout pour plusieurs raisons :
* Il n'y avait aucune activité nautique ou de loisir aquatique au lac Chauvet.
Ni en 1952, ni aujourd'hui. Comme le lac Pavin, son voisin, Chauvet est un lac de cratère où ne se pratique aucune activité de loisir de type baignade, planche à voile, et autres "jeux de plage". Le seul loisir possible, outre la promenade autour du lac, est le canotage et la pêche ... sauf justement au lac Chauvet, qui est une propriété privée. Pas de chance pour les sceptiques : de tous les lacs du Puy-de-Dôme, le lac Chauvet est justement le moins "touristique" ...
Un simple appel à l'office de tourisme du Mont-Dore suffisait à vérifier cela. Sans compter que, en 1952, les loisirs n'étaient pas du tout les mêmes qu'en 2004. Il est illusoire d'imaginer des lacs de montagne avec des plages bondées d'estivants, batifolant au milieu de parasols et de bateaux pneumatiques. On sortait encore de l'occupation, les Français étaient pauvres (le fameux "hiver 54" était encore à venir), il n'y avait encore que deux semaines de congés payés, et aucune structure d'accueil pas chère (le 1er VVF date de 1958).
* L'objet photographié ne ressemble pas du tout à un objet de plage
C'est d'une évidence effrayante mais il faut oser le rappeler. Ni par la forme, ni par la couleur (les objets de plage sont généralement de couleur vive). Il faut une indéniable mauvaise foi pour trouver une quelconque ressemblance entre l'objet photographié et un objet de loisir nautique ou balnéaire.
* bateau gonflable de plage matelas pneumatique parasol Un objet de plage n'aurait jamais pu être emporté à une telle hauteur
Un vent de 60 km/h peut secouer de grosses branches, et donc faire tourbillonner et rouler sur la plage un matelas ou un bateau gonflable léger. Mais il ne peut en aucun cas le soulever à plusieurs dizaines de mètres de haut et l'y maintenir plusieurs minues.
* J'ai posé la question à un parapentiste chevronné, connaisseur expérimenté en aérologie pratique qui me l'a confirmé. Seule une ascendence thermique puissante aurait pu faire cela. Un objet de plage emporté par le vent n'aurait jamais eu la trajectoire rapportée
Etant plus lourd que l'air il aurait inévitablement adopté une trajectoire descendante en retombant. Sans moteur en effet, il ne peut pas se sustenter, sauf s'il avait un profil d'aile (avec extrados/intrados), ce qui est assez rare pour un objet de plage ! Mais alors dans ce cas, il ne se sustenterait que grâce au vent relatif, c'est à dire que sa vitesse réelle serait nettement inférieure aux 60 km/h du vent réel, voire nulle (Cf. les mouettes qui font du sur-place par grand vent). Ceci m'a également par un aviateur confirmé.
Retour au Sommaire
Sources / Références
Optique et Photographie
Merci à Laurent Guérin pour son expérience irremplaçable du cas Chauvet.
Merci à Yves Colombe pour son aide précieuse lors de mes débuts dans la découverte de la "profondeur de champ" et du "cercle de confusion"
Merci à Joël E. pour ses critiques constructives et ses liens sur les photo-trucages.
http://members.lycos.fr/photo87/expdf.html
http://romain.bel.free.fr/agregation/Lecons/LP46.pdf
http://www.ifrance.com/philippecoubris/optique/photographie2.htm
http://astrobreuillet.free.fr/download/Gazette14.pdf
http://www.nikonlinks.com/unklbil/dof.htm
http://www.cs.mtu.edu/~shene/DigiCam/User-Guide/950/depth-of-field.html
http://www.betterphoto.com/forms/qnaDetail.asp?threadID=7062&catID=203
http://www.largeformatphotography.info/lfforum/topic/497015.html
Trucages photos / Photomontages :
http://www.rtfm.be/king/photomontage/index.html
http://home.fuse.net/arcsite/photoan2.htm
http://www.csicop.org/si/2003-09/faking-ufo-photos.html
http://www.garfnet.org.uk/new_mill/bbmedia/issue001/ufo_fake.htm
http://www.collagetown.com/ => collages photo artistiques
http://bruno.cicv.fr/etudes/semio.html
http://www.ac-reunion.fr/pedagogie/lybouvep/TPE/PremiereS/elev/trucages/comment.html
Sur le frisbee
http://www.chez.com/chamminou/c13fen05a.htm
http://inventors.about.com/library/weekly/aa980218.htm
http://inventors.about.com/gi/dynamic/offsite.htm?site=http://www.sas.it.mtu.edu/%7Edkwalika/frisbee/prohistory.html
http://www.enc.org/features/calendar/unit/0,1819,153,00.shtm
http://www.disc-wing.com/AIAA-2002-3150.pdf
http://www.disc-wing.com/CEAS_AARC_2002.pdf
Divers
Ball-trap : http://www.laporte-shooting.com
Le faux OVNI Corse dénoncé par Pierre Guérin : http://www.ifrance.com/lesrepasufologiquesparisiens/L'histoire%20des%20soucoupes%20volantes%20en%20photos.htm
http://adelmon.free.fr/Chauvet/Lac_Chauvet_5.html
Plusieurs sceptiques perspicaces ont remarqué que le nuage bas, visible sur la photo N°3, n'était plus du tout visible sur la photo N°4, ce qui paraît effectivement étrange (à première vue, on s'attendrait à en voir au moins un bout). De là à imaginer que les photos ont été prises à bien plus que 8 secondes d'intervalle ... bref, ce pourrait être un petit indice de plus en faveur du canular.
Voyons donc de quoi il retourne exactement.
Tout d'abord les 4 photos sont compatibles avec les conditions météorologiques du 18/07/1952. Les archives de la Météorologie Nationale auxquelles j'ai eu accès indiquent en effet pour ce jour là :
"Ciel clair, nébulosité = 2/10°", ce qui correspond bien à la description du témoin et aux photos : ciel uniformément bleu, avec quelques nuages bas à l'horizon (strato-cumulus, visible en photo N°4).
Sur les photos 3 et 4 l'appareil est tenu verticalement, la largeur de l'image est donc de 24 mm. Connaissant la focale on en déduit immédiatement le champ angulaire balayé par ces photos : un peu moins de 30°.
Calculons maintenant le déplacement angulaire entre les photos 3 et 4. Il se trouve que sur ces deux photos, l'objet est presque centré, et se trouve environ à 62% de largeur du cadre (ce qui est logique, André Frégnale étant un photographe quasi-pro, il a réussi à garder l'objectif pointé sur l'objet).
Donc, on peut estimer avec une très bonne approximation, que le déplacement angulaire de l'objectif, est quasiment le même que celui de l'objet. Or celui-ci se déduit très facilement des résultats de l'analyse de Pierre guérin (Cf. chapitre III) :
Db = b4 - b3
Db = 61,5° - 38° = 23,5°
Il y a donc un écart d'un peu plus de 6° (6,4 plus précisément). On devrait donc voir l'extrémité gauche du nuage de la photo N°3, sur près d'un quart de la photo N°4, en bas et à droite.
Lire au chapitre VI, l'analyse détaillée des mêmes photos par Laurent Guérin, fils de Pierre Guérin. En reprenant tous les calculs de zéro, et en tenant compte des marges d'erreur inévitables, il montre qu'il est possible de faire varier les ai et bi pour que, sans déroger au modèle mathématique de trajectoire déduit du témoignage de Frégnale, ils conduisent à une variation d'azimut suffisante pour que le nuage de la photo 3 n'apparaisse plus sur la photo 4.
La méprise avec un ballon publicitaire
A la lecture des coupures de presse que j'ai retrouvé auprès des archives de La Montagne de 1952 (voir chapitre IV), un lecteur attentif a noté l'épisode du ballon publicitaire échappé de la caravane du Tour de France le 18 juillet 1952 à l'arrivée à Vichy. Il a alors défendu avec opiniatreté l'idée que l'objet du lac Chauvet était ce ballon.
Cette hypothèse n'est pas plausible du tout.
Tout d'abord l'objet photographié n'a absolument pas l'aspect d'un ballon, a fortiori publicitaire. Ce dernier a vocation à être vu du plus grand nombre, et à rendre instantanément reconnaissable la marque dont il fait la promotion. Pour ce faire ils sont généralement très colorés et couverts d'inscriptions géantes et de logos. Or l'objet est d'une couleur uniforme (grisâtre d'après le témoin), et sans inscription.
D'autre part la trajectoire qu'aurait du suivre ce ballon parti de Vichy est totalement impossible. En effet les vents soufflaient Nord-Ouest/Sud-Est ce jour là (attesté par la météorologie nationale) à 60 km/h. Le ballon a donc du filer vers l'Est, vers St Etienne probablement.
Mon contradicteur a alors imaginé que, ayant rencontré les contreforts du massif central, le ballon les avait contourné par l'ouest, toujours en montant, pour être ensuite pris par les vents d'Ouest qui soufflaient près du lac Chauvet, et passer ainsi au-dessus d'André Frégnale (voir tracé brun sur cette carte.
Mais cela aussi est improbable. Il y a en effet un chemin bien plus naturel et plus facile pour un ballon partant de Vichy : celui de la vallée de l'Allier, puis de la Dore. Ce chemin reste à une altitude basse, et orientée Sud/Sud-Est.
Devant ces contre-arguments, mon contradicteur a généralisé son explication à "n'importe quel genre de ballon", par exemple un ballon de photographie aérienne de chantier, de provenance inconnue, et porté par le vent sur le lac Chauvet.
Et puis il s'est finalement rallié à mon opinion : seul un hasard extraordinaire (que j'ai calculé au chapitre II) aurait pu faire que la tâche sombre sous l'objet soit orientée chaque fois dans le sens de la trajectoire. Avec un objet porté par le vent (tel un ballon), cette tâche devrait logiquement avoir une position quelconque.
Retour au Sommaire
La méprise avec un objet de plage emporté par le vent
Sur la liste de discussion francom.ovni, l'ufologue sceptique Dominique Caudron a soutenu l'idée que l'objet du lac Chauvet était "évidemment" un objet de plage emporté par le vent, de type : parasol, matelas pneumatique, bateau gonflable, ballon de plage.
Cette thèse ne tient pas debout pour plusieurs raisons :
* Il n'y avait aucune activité nautique ou de loisir aquatique au lac Chauvet.
Ni en 1952, ni aujourd'hui. Comme le lac Pavin, son voisin, Chauvet est un lac de cratère où ne se pratique aucune activité de loisir de type baignade, planche à voile, et autres "jeux de plage". Le seul loisir possible, outre la promenade autour du lac, est le canotage et la pêche ... sauf justement au lac Chauvet, qui est une propriété privée. Pas de chance pour les sceptiques : de tous les lacs du Puy-de-Dôme, le lac Chauvet est justement le moins "touristique" ...
Un simple appel à l'office de tourisme du Mont-Dore suffisait à vérifier cela. Sans compter que, en 1952, les loisirs n'étaient pas du tout les mêmes qu'en 2004. Il est illusoire d'imaginer des lacs de montagne avec des plages bondées d'estivants, batifolant au milieu de parasols et de bateaux pneumatiques. On sortait encore de l'occupation, les Français étaient pauvres (le fameux "hiver 54" était encore à venir), il n'y avait encore que deux semaines de congés payés, et aucune structure d'accueil pas chère (le 1er VVF date de 1958).
* L'objet photographié ne ressemble pas du tout à un objet de plage
C'est d'une évidence effrayante mais il faut oser le rappeler. Ni par la forme, ni par la couleur (les objets de plage sont généralement de couleur vive). Il faut une indéniable mauvaise foi pour trouver une quelconque ressemblance entre l'objet photographié et un objet de loisir nautique ou balnéaire.
* bateau gonflable de plage matelas pneumatique parasol Un objet de plage n'aurait jamais pu être emporté à une telle hauteur
Un vent de 60 km/h peut secouer de grosses branches, et donc faire tourbillonner et rouler sur la plage un matelas ou un bateau gonflable léger. Mais il ne peut en aucun cas le soulever à plusieurs dizaines de mètres de haut et l'y maintenir plusieurs minues.
* J'ai posé la question à un parapentiste chevronné, connaisseur expérimenté en aérologie pratique qui me l'a confirmé. Seule une ascendence thermique puissante aurait pu faire cela. Un objet de plage emporté par le vent n'aurait jamais eu la trajectoire rapportée
Etant plus lourd que l'air il aurait inévitablement adopté une trajectoire descendante en retombant. Sans moteur en effet, il ne peut pas se sustenter, sauf s'il avait un profil d'aile (avec extrados/intrados), ce qui est assez rare pour un objet de plage ! Mais alors dans ce cas, il ne se sustenterait que grâce au vent relatif, c'est à dire que sa vitesse réelle serait nettement inférieure aux 60 km/h du vent réel, voire nulle (Cf. les mouettes qui font du sur-place par grand vent). Ceci m'a également par un aviateur confirmé.
Retour au Sommaire
Sources / Références
Optique et Photographie
Merci à Laurent Guérin pour son expérience irremplaçable du cas Chauvet.
Merci à Yves Colombe pour son aide précieuse lors de mes débuts dans la découverte de la "profondeur de champ" et du "cercle de confusion"
Merci à Joël E. pour ses critiques constructives et ses liens sur les photo-trucages.
http://members.lycos.fr/photo87/expdf.html
http://romain.bel.free.fr/agregation/Lecons/LP46.pdf
http://www.ifrance.com/philippecoubris/optique/photographie2.htm
http://astrobreuillet.free.fr/download/Gazette14.pdf
http://www.nikonlinks.com/unklbil/dof.htm
http://www.cs.mtu.edu/~shene/DigiCam/User-Guide/950/depth-of-field.html
http://www.betterphoto.com/forms/qnaDetail.asp?threadID=7062&catID=203
http://www.largeformatphotography.info/lfforum/topic/497015.html
Trucages photos / Photomontages :
http://www.rtfm.be/king/photomontage/index.html
http://home.fuse.net/arcsite/photoan2.htm
http://www.csicop.org/si/2003-09/faking-ufo-photos.html
http://www.garfnet.org.uk/new_mill/bbmedia/issue001/ufo_fake.htm
http://www.collagetown.com/ => collages photo artistiques
http://bruno.cicv.fr/etudes/semio.html
http://www.ac-reunion.fr/pedagogie/lybouvep/TPE/PremiereS/elev/trucages/comment.html
Sur le frisbee
http://www.chez.com/chamminou/c13fen05a.htm
http://inventors.about.com/library/weekly/aa980218.htm
http://inventors.about.com/gi/dynamic/offsite.htm?site=http://www.sas.it.mtu.edu/%7Edkwalika/frisbee/prohistory.html
http://www.enc.org/features/calendar/unit/0,1819,153,00.shtm
http://www.disc-wing.com/AIAA-2002-3150.pdf
http://www.disc-wing.com/CEAS_AARC_2002.pdf
Divers
Ball-trap : http://www.laporte-shooting.com
Le faux OVNI Corse dénoncé par Pierre Guérin : http://www.ifrance.com/lesrepasufologiquesparisiens/L'histoire%20des%20soucoupes%20volantes%20en%20photos.htm
http://adelmon.free.fr/Chauvet/Lac_Chauvet_5.html
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:51
VI - L’analyse des photos par Laurent Guérin
Introduction
L’étude ci-dessous est due à Laurent Guérin, le fils de Pierre
Guérin. Ingénieur lui-même, il avait notablement collaboré à l’article
de son père sur Chauvet (la version originale publiée dans le JSE le
crédite même explicitement pour son aide), en particulier pour tous les
calculs trigonométriques.
Lorsque je l’ai retrouvé puis contacté, il a très vite accepté de
“reprendre le collier”, et s’est même je crois piqué au jeu lorsque je
lui ai soumis l’anomalie du nuage. Il a repris tous les calculs en
affinant énormément la méthode, afin de tirer davantage d’informations
des photos, et de tenir compte des moindres facteurs pouvant influer
sur les calculs.
Je le remercie chaleureusement ici pour son implication et ses talents en géométrie.
Le problème de départ : l’anomalie du nuage
L’“anomalie du nuage” vient du fait que l’extrémité gauche du nuage
en bas de la photo 3 semblerait, à première vue, devoir être légèrement
visible sur la droite de la photo 4. D’après les calculs de Pierre
Guérin, Frégnale a en effet pivoté sur la gauche d’environ 23°, soit
sensiblement moins que le champ angulaire couvert par un film 35mm
(environ 30°). Voir le chapitre V du dossier Chauvet.
Bien entendu, les calculs initiaux de Pierre Guérin comportaient
des marges d’erreur non négligeables qui, cumulées, pourraient
expliquer cet écart apparent d’un peu plus de 6°. Mais pour s’en
assurer, il fallait recommencer tous les calculs depuis le début.
La méthode
Laurent Guérin a donc patiemment réalisé toutes ces mesures et tous
ces calculs. C’est avec lui que cette page a été réalisée. Pour les
matheux passionnés, toute la théorie et les équations se trouvent ici.
Retour sur l’analyse des photos du Lac Chauvet, par Laurent Guérin
Rappel de la méthode de calcul utilisée dans l’article original
Les données mesurables :
– les grands axes ai et petits axes bi des images de l’objet, dont la distorsion est corrigeable en fonction de la distance mesurable au centre de la photo ;
– les angles γi entre la trajectoire supposée de l’objet et la ligne d’horizon (photos 3 et 4 uniquement) ;
– les angles ωi entre le grand axe de l’image de l’objet et la ligne d’horizon (photos 3 et 4 uniquement) ;
– les angles γi–ωi entre la trajectoire supposée de l’objet et le grand axe de l’image de l’objet (ωi est compté ici algébriquement contrairement aux formules originales) ;
– les angles γi et ωi sur les photos 1 et 2 sont arbitrairement estimés de sorte que les valeurs γi–ωi soient compatibles avec leurs mesures.
Les formules utilisées :
On trouvera la démonstration des formules, plus complète que celle donnée dans l’article original, ici.
L’aplatissement ri est donné par bi/ai.
(1) sinαi/ai = cste ;
(2) cosβi = tgαi/tgα0 ;
(3) tgγi = –sinαi.tgβi (βi est compté ici négativement à gauche de l’observateur contrairement aux formules originales) ;
(4) tgαi = ri.(1–ri2)–½.sinγi/sin(γi–ωi) ;
(5) (1–ri2)½.sinωi = sinΩi.sinβi (Ωi
est compté positivement quand l’objet s’incline de manière à paraître
plus circulaire à l’observateur, comme dans les formules originales) ;
Une autre formule importante n’était pas explicitée dans l’article original :
(6) ri = sinαi.cosΩi+cosαi.sinΩi.cosβi.
Le résumé de la méthode de calcul originale :
On part des mesures les plus fiables (photo 3) r3, γ3 et ω3 pour en déduire selon (4) α3.
Une valeur de α4 est obtenue selon le même principe, car les valeurs ont une fiabilité correcte.
La formule (1) permet d’en déduire les autres αi ; on constate une excellente concordance entre les deux valeurs obtenues de α4 ; on constate aussi que les valeurs de αi pour les photos 1 et 2 sont cohérentes avec celles obtenues selon (4) avec les estimations arbitraires de γi et de ωi.
Comme il est estimé que β2 est voisin de zéro, une estimation de Ω2 est donnée à l’aide de α2 et r2. Cela correspond en fait à utiliser (6) qui devient ici r2 = sin(α2+Ω2).
Le calcul plus précis de β2 est alors obtenu grâce à (5) ; (2) conduit alors à α0.
Cette même formule (2) conduit alors aux autres βi, puis les autres Ωi sont alors déduits de (5).
La cohérence des valeurs obtenues (utilisation d’un α moyen
entre les photos 1 et 2) est vérifiée pour comparer l’écart angulaire
calculé entre ces deux photos et la mesure de cet écart sur une photo
composite.
Amélioration de cette méthode de calcul
Constat : il est possible de calculer précisément l’écart angulaire χ entre les positions 1 et 2.
En effet, à partir des mesures des positions d’un certain nombre de
points caractéristiques de l’arbre (visibles sur les photos 1 et 2), il
est possible de calculer la transformation permettant de passer d’un
repère lié à la photo 1 à un repère lié à la photo 2.
A partir des mesures de l’objet sur la photo 1, il est possible de
calculer la direction de l’objet dans le repère de la photo 1, puis par
la transformation ci-dessus, de calculer cette direction dans le repère
de la photo 2 (qui représente la position qu’aurait eue l’objet sur la
photo 2 s’il n’avait pas bougé). De même, à partir des mesures de
l’objet sur la photo 2, il est possible de calculer la direction de
l’objet dans le repère de la photo 2. L’écart angulaire entre les deux
positions est obtenu par le produit scalaire entre les deux directions
calculées dans le repère de la photo 2.
Deux jeux de test sur des points caractéristiques différents
conduisent à des valeurs extrêmement voisines, prouvant la fiabilité et
la précision de ce calcul et donc de l’écart calculé. On trouve χ = 13.75° ±0.05°.
Application pratique avec cinq points mesurés :
Comme expliqué dans l’annexe (ici), la transformation est caractérisée par trois paramètres λ, η et ω,
qui doivent être déterminés de manière à optimiser l’ajustement des
points caractéristiques de la photo 1 sur la photo 2. (Cet ω n’a rien à voir avec l’angle entre le grand axe de l’image de l’objet et la ligne d’horizon sur les photos.)
Le formulaire ci-dessous permet de calculer, pour chacun des paramètres, la meilleure valeur x autour d’une valeur approximative initiale x0, parmi les valeur xn = x0+n.δx,
avec –10 ≤ n ≤ 10. Ce processus peut être répété plusieurs fois en
prenant la valeur obtenue à une étape comme valeur initiale de l’étape
suivante et en diminuant l’incrément, de manière à affiner le résultat.
On entre les mesures des points caractéristiques d1i et d2i, φ1i et φ2i, les valeurs θ1i et θ2i seront automatiquement calculées.
On entre les mesures de l’objet d1 et d2, φ1 et φ2, les valeurs θ1 et θ2 seront automatiquement calculées.
On entre une valeur approximative pour λ, η et ω,
et des incréments de test pour ces paramètres. Une méthode graphique
d’évaluation des valeurs initiales est expliquée plus bas.
Le bouton lance alors l’optimisation, et l’écart angulaire χ
est automatiquement calculé. Il est possible d’affiner le résultat à
partir des valeurs ainsi trouvées en diminuant les incréments de test
(attention à bien mettre des points et non des virgules aux nombres
décimaux).Distance focale (en mm) :
Position de la feuille i sur la photo 1 :
Distance au centre d1i (en mm) :
Ecart angulaire / axe de visée θ1i (en °) :
Orientation / grand côté φ1i (en °) :
Position de la feuille i sur la photo 2 :
Distance au centre d2i (en mm) :
Ecart angulaire / axe de visée θ2i (en °) :
Orientation / grand côté φ2i (en °) :
Paramètres de la transformation 1 vers 2 :
Ecart angulaire λ entre axes de visée 1 et 2 ; Incrément de test (en °) :
Orientation η axe de visée 2 / grand côté 1 ; Incrément de test (en °) :
Rotation ω photo 2 / photo 1 ; Incrément de test (en °) :
Position de l’objet sur la photo k :
Distance au centre dk (en mm) :
Ecart angulaire / axe de visée θk (en °) :
Orientation / grand côté φk (en °) :
Cliquez sur pour obtenir l’écart angulaire :
Ecart angulaire χ entre les positions 1 et 2 (en °) :
Introduction
L’étude ci-dessous est due à Laurent Guérin, le fils de Pierre
Guérin. Ingénieur lui-même, il avait notablement collaboré à l’article
de son père sur Chauvet (la version originale publiée dans le JSE le
crédite même explicitement pour son aide), en particulier pour tous les
calculs trigonométriques.
Lorsque je l’ai retrouvé puis contacté, il a très vite accepté de
“reprendre le collier”, et s’est même je crois piqué au jeu lorsque je
lui ai soumis l’anomalie du nuage. Il a repris tous les calculs en
affinant énormément la méthode, afin de tirer davantage d’informations
des photos, et de tenir compte des moindres facteurs pouvant influer
sur les calculs.
Je le remercie chaleureusement ici pour son implication et ses talents en géométrie.
Le problème de départ : l’anomalie du nuage
L’“anomalie du nuage” vient du fait que l’extrémité gauche du nuage
en bas de la photo 3 semblerait, à première vue, devoir être légèrement
visible sur la droite de la photo 4. D’après les calculs de Pierre
Guérin, Frégnale a en effet pivoté sur la gauche d’environ 23°, soit
sensiblement moins que le champ angulaire couvert par un film 35mm
(environ 30°). Voir le chapitre V du dossier Chauvet.
Bien entendu, les calculs initiaux de Pierre Guérin comportaient
des marges d’erreur non négligeables qui, cumulées, pourraient
expliquer cet écart apparent d’un peu plus de 6°. Mais pour s’en
assurer, il fallait recommencer tous les calculs depuis le début.
La méthode
- Idéalement il faudrait prendre un point à l’extrémité gauche du nuage de la photo 3, et calculer ses coordonnées (x, y)
sur la photo 4. Si ces coordonnées, malgré les marges d’erreur
résultantes, restaient à l’intérieur du cadre 24x36 de la photo 4,
alors c’est qu’il y a bien “anomalie”, et donc un fort soupçon de
trucage de l’une au moins de ces deux photos. - Il convient donc de déterminer les formules permettant de calculer ces coordonnées linéaires (x, y) en fonction de coordonnées angulaires de hauteur angulaire et d’azimut (α, β), en tenant compte de la distorsion radiale.
- Or le calcul de βi en fonction de αi et α0 est très sensible à α0, surtout pour les photos 1 et 2, car cosβi est proche de 1.
- Ce qu’il convient de faire est donc de tester α0
de sorte que l’angle entre les directions de l’objet sur les photos 1
et 2 coïncide avec la valeur que l’on peut mesurer sur une photo
composite (obtenue grâce à l’arbre). - Une première donnée à mesurer ou à calculer avec une assez
grande précision est donc l’angle entre les deux directions de l’objet
sur ces deux photos.
Laurent Guérin a donc patiemment réalisé toutes ces mesures et tous
ces calculs. C’est avec lui que cette page a été réalisée. Pour les
matheux passionnés, toute la théorie et les équations se trouvent ici.
Retour sur l’analyse des photos du Lac Chauvet, par Laurent Guérin
Rappel de la méthode de calcul utilisée dans l’article original
Les données mesurables :
– les grands axes ai et petits axes bi des images de l’objet, dont la distorsion est corrigeable en fonction de la distance mesurable au centre de la photo ;
– les angles γi entre la trajectoire supposée de l’objet et la ligne d’horizon (photos 3 et 4 uniquement) ;
– les angles ωi entre le grand axe de l’image de l’objet et la ligne d’horizon (photos 3 et 4 uniquement) ;
– les angles γi–ωi entre la trajectoire supposée de l’objet et le grand axe de l’image de l’objet (ωi est compté ici algébriquement contrairement aux formules originales) ;
– les angles γi et ωi sur les photos 1 et 2 sont arbitrairement estimés de sorte que les valeurs γi–ωi soient compatibles avec leurs mesures.
Les formules utilisées :
On trouvera la démonstration des formules, plus complète que celle donnée dans l’article original, ici.
L’aplatissement ri est donné par bi/ai.
(1) sinαi/ai = cste ;
(2) cosβi = tgαi/tgα0 ;
(3) tgγi = –sinαi.tgβi (βi est compté ici négativement à gauche de l’observateur contrairement aux formules originales) ;
(4) tgαi = ri.(1–ri2)–½.sinγi/sin(γi–ωi) ;
(5) (1–ri2)½.sinωi = sinΩi.sinβi (Ωi
est compté positivement quand l’objet s’incline de manière à paraître
plus circulaire à l’observateur, comme dans les formules originales) ;
Une autre formule importante n’était pas explicitée dans l’article original :
(6) ri = sinαi.cosΩi+cosαi.sinΩi.cosβi.
Le résumé de la méthode de calcul originale :
On part des mesures les plus fiables (photo 3) r3, γ3 et ω3 pour en déduire selon (4) α3.
Une valeur de α4 est obtenue selon le même principe, car les valeurs ont une fiabilité correcte.
La formule (1) permet d’en déduire les autres αi ; on constate une excellente concordance entre les deux valeurs obtenues de α4 ; on constate aussi que les valeurs de αi pour les photos 1 et 2 sont cohérentes avec celles obtenues selon (4) avec les estimations arbitraires de γi et de ωi.
Comme il est estimé que β2 est voisin de zéro, une estimation de Ω2 est donnée à l’aide de α2 et r2. Cela correspond en fait à utiliser (6) qui devient ici r2 = sin(α2+Ω2).
Le calcul plus précis de β2 est alors obtenu grâce à (5) ; (2) conduit alors à α0.
Cette même formule (2) conduit alors aux autres βi, puis les autres Ωi sont alors déduits de (5).
La cohérence des valeurs obtenues (utilisation d’un α moyen
entre les photos 1 et 2) est vérifiée pour comparer l’écart angulaire
calculé entre ces deux photos et la mesure de cet écart sur une photo
composite.
Amélioration de cette méthode de calcul
Constat : il est possible de calculer précisément l’écart angulaire χ entre les positions 1 et 2.
En effet, à partir des mesures des positions d’un certain nombre de
points caractéristiques de l’arbre (visibles sur les photos 1 et 2), il
est possible de calculer la transformation permettant de passer d’un
repère lié à la photo 1 à un repère lié à la photo 2.
A partir des mesures de l’objet sur la photo 1, il est possible de
calculer la direction de l’objet dans le repère de la photo 1, puis par
la transformation ci-dessus, de calculer cette direction dans le repère
de la photo 2 (qui représente la position qu’aurait eue l’objet sur la
photo 2 s’il n’avait pas bougé). De même, à partir des mesures de
l’objet sur la photo 2, il est possible de calculer la direction de
l’objet dans le repère de la photo 2. L’écart angulaire entre les deux
positions est obtenu par le produit scalaire entre les deux directions
calculées dans le repère de la photo 2.
Deux jeux de test sur des points caractéristiques différents
conduisent à des valeurs extrêmement voisines, prouvant la fiabilité et
la précision de ce calcul et donc de l’écart calculé. On trouve χ = 13.75° ±0.05°.
Application pratique avec cinq points mesurés :
Comme expliqué dans l’annexe (ici), la transformation est caractérisée par trois paramètres λ, η et ω,
qui doivent être déterminés de manière à optimiser l’ajustement des
points caractéristiques de la photo 1 sur la photo 2. (Cet ω n’a rien à voir avec l’angle entre le grand axe de l’image de l’objet et la ligne d’horizon sur les photos.)
Le formulaire ci-dessous permet de calculer, pour chacun des paramètres, la meilleure valeur x autour d’une valeur approximative initiale x0, parmi les valeur xn = x0+n.δx,
avec –10 ≤ n ≤ 10. Ce processus peut être répété plusieurs fois en
prenant la valeur obtenue à une étape comme valeur initiale de l’étape
suivante et en diminuant l’incrément, de manière à affiner le résultat.
On entre les mesures des points caractéristiques d1i et d2i, φ1i et φ2i, les valeurs θ1i et θ2i seront automatiquement calculées.
On entre les mesures de l’objet d1 et d2, φ1 et φ2, les valeurs θ1 et θ2 seront automatiquement calculées.
On entre une valeur approximative pour λ, η et ω,
et des incréments de test pour ces paramètres. Une méthode graphique
d’évaluation des valeurs initiales est expliquée plus bas.
Le bouton lance alors l’optimisation, et l’écart angulaire χ
est automatiquement calculé. Il est possible d’affiner le résultat à
partir des valeurs ainsi trouvées en diminuant les incréments de test
(attention à bien mettre des points et non des virgules aux nombres
décimaux).Distance focale (en mm) :
Position de la feuille i sur la photo 1 :
Distance au centre d1i (en mm) :
Ecart angulaire / axe de visée θ1i (en °) :
Orientation / grand côté φ1i (en °) :
Position de la feuille i sur la photo 2 :
Distance au centre d2i (en mm) :
Ecart angulaire / axe de visée θ2i (en °) :
Orientation / grand côté φ2i (en °) :
Paramètres de la transformation 1 vers 2 :
Ecart angulaire λ entre axes de visée 1 et 2 ; Incrément de test (en °) :
Orientation η axe de visée 2 / grand côté 1 ; Incrément de test (en °) :
Rotation ω photo 2 / photo 1 ; Incrément de test (en °) :
Position de l’objet sur la photo k :
Distance au centre dk (en mm) :
Ecart angulaire / axe de visée θk (en °) :
Orientation / grand côté φk (en °) :
Cliquez sur pour obtenir l’écart angulaire :
Ecart angulaire χ entre les positions 1 et 2 (en °) :
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:52
Obtention graphique des paramètres dk, dki, φk, φki, λ, η et ω :
et de l’objet sur chaque photo, mais sans doute approximatives pour les
paramètres de la transformation, qui sont initialisées dans le
formulaire plus haut.
Les valeurs des paramètres de la transformation sont a priori
approximatives non seulement parce que la procédure d’ajustement est
manuelle au sein d’un logiciel de dessin, mais aussi parce que les
éléments que l’on déplace d’une photo à l’autre devraient eux-mêmes
être distordus lors du déplacement puisque les centres ne coïncident
pas, ce qui n’est pas réalisé dans le processus décrit ci-dessus. D’où
la nécessité de procéder à une optimisation mathématiquement rigoureuse
implémentée dans le précédent formulaire.
Une première passe avec un incrément de 0,5° conduit à λ = 10,9°, η = –180,1° et ω = –22,7°. En diminuant l’incrément à 0,1°, on obtient alors λ = 11,0°, η = –179,7° et ω = –22,9°. En diminuant l’incrément à 0,01°, on obtient finalement, après une deuxième passe de contrôle, λ = 10,98°, η = –179,81° et ω = –22,88°, et enfin χ = 13,77°.
Il est intéressant de constater cependant que l’on peut tout de
même, par ces manipulations graphiques, obtenir une estimation directe
de l’écart angulaire entre les deux positions de l’objet. En effet, sur
la photo 1 composite, on constate que le vecteur déplacement est
quasiment radial. En mesurant la longueur d du trait magenta (= 11,31 mm), on peut considérer que tg(θ1+χ) = (d1+d)/f, ce qui donne l’estimation χ = 13,5° environ, valeur extrêmement voisine de celle donnée par le calcul théorique précis avec distorsions.
Une méthode de calcul modifiée :
Le constat plus haut est mis à profit pour dériver de manière
différente les paramètres angulaires. En effet, Les premières étapes de
cette méthode modifiée sont identiques : α3 et α4 sont toujours déterminées grâce à (4), tandis que α1 et α2 sont déterminées d’après α3 grâce à (1).
Pour les photos 1 et 2, αi est donc fonction de ai, a3 et α3. Comme expliqué dans l’annexe (ici), il se trouve que α0 est fonction de α1, α2 et de l’écart angulaire χ entre les positions 1 et 2. Donc α0 est entièrement déterminé par a1, a2, a3, α3 et χ.
La formule (2) permet alors de déterminer les βi, puis (3) permet de déterminer les γi, puis (4) permet de déterminer les ωi, et enfin (5) permet de déterminer les Ωi.
Constat : il est possible de calculer précisément la
position du nuage sur la photo 4, ainsi que celle de l’horizon sur les
photos 3 et 4.
En effet, comme expliqué en annexe (ici),
premièrement, connaissant la hauteur angulaire et l’azimut d’un point
sur une photo et la position de ce point par rapport au centre de cette
photo, il est possible de calculer la hauteur angulaire et l’azimut de
l’axe de visée de cette photo ; deuxièmement, connaissant la hauteur
angulaire et l’azimut de l’axe de visée d’une photo et la position d’un
point par rapport au centre de cette photo, il est possible de calculer
la hauteur angulaire et l’azimut de ce point ; et enfin troisièmement,
connaissant la hauteur angulaire et l’azimut d’un point et la hauteur
angulaire et l’azimut de l’axe de visée d’une photo, il est possible de
calculer la position qu’aurait ce point sur cette photo.
Connaissant la hauteur angulaire et l’azimut de l’objet sur la
photo 3, on mesure donc sa position pour en déduire la hauteur
angulaire et l’azimut de l’axe de visée de cette photo, puis on mesure
la position du nuage sur cette photo pour en déduire sa hauteur
angulaire et son azimut.
Connaissant la hauteur angulaire et l’azimut de l’objet sur la
photo 4, on mesure ensuite sa position pour en déduire la hauteur
angulaire et l’azimut de l’axe de visée de cette photo, ce qui permet
enfin de calculer la position du nuage sur cette photo, puisqu’on
connaît sa hauteur angulaire et son azimut.
Connaissant la hauteur angulaire de l’axe de visée d’une photo, on
en déduit la position de l’horizon sur cette photo, puisqu’on connaît
sa hauteur angulaire, qui est nulle.
Les mesures des positions sont effectuées dans un repère centré
sur l’axe de visée et orienté selon les hauteurs angulaires et les
azimuts, directions estimées d’après le nuage sur la photo 3 et d’après
le talus sur la photo 4.
Application et détermination des paramètres :
Le formulaire ci-dessous permet de réaliser tous les calculs
ci-dessus (attention à bien mettre des points et non des virgules aux
nombres décimaux).Distance focale (en mm) :
Ecart angulaire χ entre positions 1 et 2 (en °) :
Cliquez sur pour calculer les paramètres :
Hauteur angulaire maximale α0 (en °) :
Largueur angulaire maximale 2ε0 (en °) :
Distance au centre dk (en mm) :
Ecart angulaire / axe de visée θk (en °) :
Grand axe (mesure brute) 2a'k (en mm) :
Petit axe (mesure brute) 2b'k (en mm) :
Grand axe (après correction) 2ak (en mm) :
Petit axe (après correction) 2bk (en mm) :
Aplatissement rk :
Largeur angulaire 2εk (en °) :
Orientation trajectoire / horizon γk (en °) :
Orientation grand axe / horizon ωk (en °) :
Angle trajectoire / grand axe γk–ωk (en °) :
et de l’objet sur chaque photo, mais sans doute approximatives pour les
paramètres de la transformation, qui sont initialisées dans le
formulaire plus haut.
Les valeurs des paramètres de la transformation sont a priori
approximatives non seulement parce que la procédure d’ajustement est
manuelle au sein d’un logiciel de dessin, mais aussi parce que les
éléments que l’on déplace d’une photo à l’autre devraient eux-mêmes
être distordus lors du déplacement puisque les centres ne coïncident
pas, ce qui n’est pas réalisé dans le processus décrit ci-dessus. D’où
la nécessité de procéder à une optimisation mathématiquement rigoureuse
implémentée dans le précédent formulaire.
Une première passe avec un incrément de 0,5° conduit à λ = 10,9°, η = –180,1° et ω = –22,7°. En diminuant l’incrément à 0,1°, on obtient alors λ = 11,0°, η = –179,7° et ω = –22,9°. En diminuant l’incrément à 0,01°, on obtient finalement, après une deuxième passe de contrôle, λ = 10,98°, η = –179,81° et ω = –22,88°, et enfin χ = 13,77°.
Il est intéressant de constater cependant que l’on peut tout de
même, par ces manipulations graphiques, obtenir une estimation directe
de l’écart angulaire entre les deux positions de l’objet. En effet, sur
la photo 1 composite, on constate que le vecteur déplacement est
quasiment radial. En mesurant la longueur d du trait magenta (= 11,31 mm), on peut considérer que tg(θ1+χ) = (d1+d)/f, ce qui donne l’estimation χ = 13,5° environ, valeur extrêmement voisine de celle donnée par le calcul théorique précis avec distorsions.
Une méthode de calcul modifiée :
Le constat plus haut est mis à profit pour dériver de manière
différente les paramètres angulaires. En effet, Les premières étapes de
cette méthode modifiée sont identiques : α3 et α4 sont toujours déterminées grâce à (4), tandis que α1 et α2 sont déterminées d’après α3 grâce à (1).
Pour les photos 1 et 2, αi est donc fonction de ai, a3 et α3. Comme expliqué dans l’annexe (ici), il se trouve que α0 est fonction de α1, α2 et de l’écart angulaire χ entre les positions 1 et 2. Donc α0 est entièrement déterminé par a1, a2, a3, α3 et χ.
La formule (2) permet alors de déterminer les βi, puis (3) permet de déterminer les γi, puis (4) permet de déterminer les ωi, et enfin (5) permet de déterminer les Ωi.
Constat : il est possible de calculer précisément la
position du nuage sur la photo 4, ainsi que celle de l’horizon sur les
photos 3 et 4.
En effet, comme expliqué en annexe (ici),
premièrement, connaissant la hauteur angulaire et l’azimut d’un point
sur une photo et la position de ce point par rapport au centre de cette
photo, il est possible de calculer la hauteur angulaire et l’azimut de
l’axe de visée de cette photo ; deuxièmement, connaissant la hauteur
angulaire et l’azimut de l’axe de visée d’une photo et la position d’un
point par rapport au centre de cette photo, il est possible de calculer
la hauteur angulaire et l’azimut de ce point ; et enfin troisièmement,
connaissant la hauteur angulaire et l’azimut d’un point et la hauteur
angulaire et l’azimut de l’axe de visée d’une photo, il est possible de
calculer la position qu’aurait ce point sur cette photo.
Connaissant la hauteur angulaire et l’azimut de l’objet sur la
photo 3, on mesure donc sa position pour en déduire la hauteur
angulaire et l’azimut de l’axe de visée de cette photo, puis on mesure
la position du nuage sur cette photo pour en déduire sa hauteur
angulaire et son azimut.
Connaissant la hauteur angulaire et l’azimut de l’objet sur la
photo 4, on mesure ensuite sa position pour en déduire la hauteur
angulaire et l’azimut de l’axe de visée de cette photo, ce qui permet
enfin de calculer la position du nuage sur cette photo, puisqu’on
connaît sa hauteur angulaire et son azimut.
Connaissant la hauteur angulaire de l’axe de visée d’une photo, on
en déduit la position de l’horizon sur cette photo, puisqu’on connaît
sa hauteur angulaire, qui est nulle.
Les mesures des positions sont effectuées dans un repère centré
sur l’axe de visée et orienté selon les hauteurs angulaires et les
azimuts, directions estimées d’après le nuage sur la photo 3 et d’après
le talus sur la photo 4.
Application et détermination des paramètres :
Le formulaire ci-dessous permet de réaliser tous les calculs
ci-dessus (attention à bien mettre des points et non des virgules aux
nombres décimaux).Distance focale (en mm) :
Ecart angulaire χ entre positions 1 et 2 (en °) :
Cliquez sur pour calculer les paramètres :
Hauteur angulaire maximale α0 (en °) :
Largueur angulaire maximale 2ε0 (en °) :
Distance au centre dk (en mm) :
Ecart angulaire / axe de visée θk (en °) :
Grand axe (mesure brute) 2a'k (en mm) :
Petit axe (mesure brute) 2b'k (en mm) :
Grand axe (après correction) 2ak (en mm) :
Petit axe (après correction) 2bk (en mm) :
Aplatissement rk :
Largeur angulaire 2εk (en °) :
Orientation trajectoire / horizon γk (en °) :
Orientation grand axe / horizon ωk (en °) :
Angle trajectoire / grand axe γk–ωk (en °) :
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:52
Hauteur angulaire αk (en °) :
Azimut βk (en °) :
Recalcul trajectoire / horizon γk (en °) :
Recalcul grand axe / horizon ωk (en °) :
Recalcul trajectoire / grand axe γk–ωk (en °) :
Inclinaison / trajectoire Ωk (en °) :
Instant de prise de vue tk (en τ*) :
Ascisse objet xOk (en mm) :
Ordonnée objet yOk (en mm) :
Hauteur angulaire centre αCk (en °) :
Azimut centre βCk (en °) :
Ascisse nuage xNk (en mm) :
Ordonnée nuage yNk (en mm) :
Hauteur angulaire nuage αN (en °) :
Azimut nuage βN (en °) :
Ordonnée horizon yHk (en mm) :
* Unité de temps représentant la durée que met l’objet pour parcourir son rayon.
On constate qu’effectivement le nuage devrait être visible sur la photo 4 (xN4 = 8,50mm) avec les valeurs calculées d’après les mesures de l’article original.
Cependant, on constate qu’en faisant varier dans les intervalles
définis par les incertitudes mentionnées dans l’article original les
grand et petit axes, ou les angles de la trajectoire et du grand axe
par rapport à l’horizon pour les photos 3 et 4, on obtient alors des
variations conséquentes pour les différents paramètres, et en
particulier pour l’abscisse du nuage sur la photo 4. On peut donc dire
que cette méthode de calcul est très sensible aux incertitudes.
Rappel des incertitudes originales sur les valeurs brutes :
Prenons par exemple les valeurs brutes extrêmes suivantes :
On constate cette fois-ci que le nuage est bien invisible sur la photo 4 (xN4 = 12,63mm). L’horizon quant à lui n’est pas modifié et est bien sous le talus (yH4
= –14,49mm). Mais il peut y avoir d’autres choix permettant ce
résultat. Sur les photos 3 et 4 ci-dessous (cliquez pour agrandir), les
traits jaunes représentent le système de coordonnées redressé, les
traits magenta indiquent la position du nuage et le trait vert celle de
l’horizon. Sur la photo 4, les positions du nuage avec les valeurs
originales de l’article (anomalie) et le nouveau jeu de test sont
représentées.
Nous venons de voir comment expliquer le fait que le nuage ne soit
pas visible sur la photo 4 : sa position calculée est extrêmement
sensible aux choix des mesures dans leur intervalle d’incertitude. Mais
le test ci-dessus n’était qu’un exemple ; encore faut-il aussi que tous
les autres paramètres recalculés après coup soient eux aussi cohérents
avec leurs mesures (en particulier les angles γ et ω).
Commentaire sur l’interdépendance des mesures :
Ce dernier point mérite d’être commenté : en effet, le formulaire
ci-dessus donne pour ces deux angles des valeurs recalculées
différentes des valeurs initiales mesurées. Ceci vient du fait que le
système d’équations est surdéterminant si l’on considère r, γ et ω comme des paramètres et α et β comme des inconnues. Plus précisément, on a dans ce cas 17 paramètres (les ai, ri, γi et ωi ainsi que χ) et 13 inconnues (les αi, βi et Ωi ainsi que α0), tandis qu’on a 20 équations (3 de type (1)*, 4 de type (2), (3), (4), (5) ou (6)**, ainsi que la relation reliant χ à α1, α2, β1 et β2).
Il est donc patent que les mesures des paramètres ne peuvent être
considérées comme indépendantes et que toutes les équations ne peuvent
être vérifiées simultanément avec des choix de valeurs mesurées
quelconques.
* sin αp/ap = sin αq/aq conduit bien à trois équations indépendantes en faisant varier p et q.
** Les équations (4), (5) et (6) ne sont en effet pas indépendantes.
Si les conditions des mesures étaient telles qu’elles
conduisaient à des incertitudes minimes sur tous les paramètres, alors
cela invaliderait le modèle mathématique. Or il se trouve que les
mesures, en particulier celles de γ et ω sont entachées
de larges incertitudes. Il convient donc de les utiliser a minima dans
la dérivation des paramètres et de favoriser les autres mesures, comme
celles de a et r, et surtout χ. C’est ce que nous avons fait dans le formulaire, où γ3 et ω3 sont utilisés une seule fois au départ pour calculer α3, puis recalculés à la fin une fois tous les autres paramètres déterminés.
Si l’on considère maintenant les γi et ωi comme des inconnues et si l’on rajoute un paramètre a0
(en relation directe avec la largeur angulaire maximale), il se rajoute
une quatrième équation de type (1), et l’on obtient un système de 21
équations à 21 inconnues et 10 paramètres. Le choix de ce qui joue le
rôle de paramètre et celui d’inconnue est d’ailleurs totalement
arbitraire : on peut soit tenter de résoudre les équations en fonction
des données mesurées (méthode directe), ou bien attribuer des valeurs
test à des inconnues et calculer quelles devraient alors être les
valeurs mesurées, et les comparer aux mesures effectives, ou bien même
une méthode mixte.
Une nouvelle méthode de calcul :
Il s’avère que cette dernière méthode est la plus efficace et facile
à mettre en œuvre : nous posons comme valeurs test les azimuts βi et les aplatissements ri, ainsi que la largeur angulaire maximale 2ε0, ce qui permet de calculer tous les autres paramètres angulaires ou dimensionnels. Le choix des βi comme valeurs de test vient de ce que cela conduit à une moindre sensibilité aux variations.
La procédure est la suivante : (2) fournit αi en fonction de α0 et βi ; χ étant fonction de α1, α2, βi et β2, χ est fonction de α0, β1 et β2 ; par inversion, α0 est fonction de χ, β1 et β2, et donc αi est fonction de χ et des βk. (3) fournit γi en fonction de χ et des βk. L’inversion de (6) fournit Ωi en fonction de χ, ri et des βk. (5) fournit ωi en fonction de χ, ri et des βk.
On peut contrôler que (4) est bien vérifiée, preuve que les équations
étaient dépendantes et qu’on ne pouvait pas attribuer des valeurs
mesurées quelconques à la fois à r, γi et ωi. Le paramètre ε0 permet enfin avec (1) de trouver ai en fonction de ε0, χ et des βk (et bien sûr de la distance focale f), puis de trouver bi en fonction de ε0, χ et des βk.
La simple donnée de valeurs test pour les βi permet donc de déduire les αi et les γi ; la donnée de valeurs mesurées et corrigées pour les ri permet de déduire les Ωi et les ωi ; la donnée d’une valeur test pour ε0 permet de déduire les ai et les bi.
Le jeu de test permet aussi de calculer la position du nuage et de
l’horizon sur la photo 4 et donc de le valider ou non. Il faut ensuite
que les valeurs trouvées pour γ–ω soient compatibles avec celles mesurées sur les photos 3 et 4 où la mesure est fiable, et que les valeurs a et b soient cohérentes avec celles mesurées après correction de distorsion.
Azimut βk (en °) :
Recalcul trajectoire / horizon γk (en °) :
Recalcul grand axe / horizon ωk (en °) :
Recalcul trajectoire / grand axe γk–ωk (en °) :
Inclinaison / trajectoire Ωk (en °) :
Instant de prise de vue tk (en τ*) :
Ascisse objet xOk (en mm) :
Ordonnée objet yOk (en mm) :
Hauteur angulaire centre αCk (en °) :
Azimut centre βCk (en °) :
Ascisse nuage xNk (en mm) :
Ordonnée nuage yNk (en mm) :
Hauteur angulaire nuage αN (en °) :
Azimut nuage βN (en °) :
Ordonnée horizon yHk (en mm) :
* Unité de temps représentant la durée que met l’objet pour parcourir son rayon.
On constate qu’effectivement le nuage devrait être visible sur la photo 4 (xN4 = 8,50mm) avec les valeurs calculées d’après les mesures de l’article original.
Cependant, on constate qu’en faisant varier dans les intervalles
définis par les incertitudes mentionnées dans l’article original les
grand et petit axes, ou les angles de la trajectoire et du grand axe
par rapport à l’horizon pour les photos 3 et 4, on obtient alors des
variations conséquentes pour les différents paramètres, et en
particulier pour l’abscisse du nuage sur la photo 4. On peut donc dire
que cette méthode de calcul est très sensible aux incertitudes.
Rappel des incertitudes originales sur les valeurs brutes :
| 2a'1 = 0,845±0,030 | 2a'2 = 0,873±0,025 | 2a'3 = 0,751±0,015 | 2a'4 = 0,544±0,015 |
| 2b'1 = 0,720±0,015 | 2b'2 = 0,702±0,015 | 2b'3 = 0,528±0,015 | 2b'4 = 0,286±0,015 |
| γ3 = 26,0°±1,5° | γ4 = 41,0°±3,0° | ||
| ω3 = –4,0°±0,5° | ω4 = –9,0°±1,0° | ||
| γ1–ω1 = –16,0°±2,0° | γ2–ω2 = 4,0°±0,5° |
Prenons par exemple les valeurs brutes extrêmes suivantes :
| 2a'1 = 0,815 | 2a'2 = 0,848 | 2a'3 = 0,766 | 2a'4 = 0,559 |
| 2b'1 = 0,705 | 2b'2 = 0,717 | 2b'3 = 0,543 | 2b'4 = 0,301 |
| γ3 = 24,5° | γ4 = 38,0° | ||
| ω3 = –4,5° | ω4 = –10,0° |
On constate cette fois-ci que le nuage est bien invisible sur la photo 4 (xN4 = 12,63mm). L’horizon quant à lui n’est pas modifié et est bien sous le talus (yH4
= –14,49mm). Mais il peut y avoir d’autres choix permettant ce
résultat. Sur les photos 3 et 4 ci-dessous (cliquez pour agrandir), les
traits jaunes représentent le système de coordonnées redressé, les
traits magenta indiquent la position du nuage et le trait vert celle de
l’horizon. Sur la photo 4, les positions du nuage avec les valeurs
originales de l’article (anomalie) et le nouveau jeu de test sont
représentées.
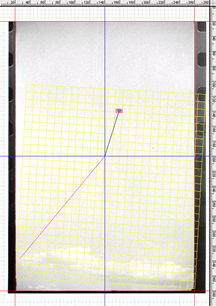 |  |
Nous venons de voir comment expliquer le fait que le nuage ne soit
pas visible sur la photo 4 : sa position calculée est extrêmement
sensible aux choix des mesures dans leur intervalle d’incertitude. Mais
le test ci-dessus n’était qu’un exemple ; encore faut-il aussi que tous
les autres paramètres recalculés après coup soient eux aussi cohérents
avec leurs mesures (en particulier les angles γ et ω).
Commentaire sur l’interdépendance des mesures :
Ce dernier point mérite d’être commenté : en effet, le formulaire
ci-dessus donne pour ces deux angles des valeurs recalculées
différentes des valeurs initiales mesurées. Ceci vient du fait que le
système d’équations est surdéterminant si l’on considère r, γ et ω comme des paramètres et α et β comme des inconnues. Plus précisément, on a dans ce cas 17 paramètres (les ai, ri, γi et ωi ainsi que χ) et 13 inconnues (les αi, βi et Ωi ainsi que α0), tandis qu’on a 20 équations (3 de type (1)*, 4 de type (2), (3), (4), (5) ou (6)**, ainsi que la relation reliant χ à α1, α2, β1 et β2).
Il est donc patent que les mesures des paramètres ne peuvent être
considérées comme indépendantes et que toutes les équations ne peuvent
être vérifiées simultanément avec des choix de valeurs mesurées
quelconques.
* sin αp/ap = sin αq/aq conduit bien à trois équations indépendantes en faisant varier p et q.
** Les équations (4), (5) et (6) ne sont en effet pas indépendantes.
Si les conditions des mesures étaient telles qu’elles
conduisaient à des incertitudes minimes sur tous les paramètres, alors
cela invaliderait le modèle mathématique. Or il se trouve que les
mesures, en particulier celles de γ et ω sont entachées
de larges incertitudes. Il convient donc de les utiliser a minima dans
la dérivation des paramètres et de favoriser les autres mesures, comme
celles de a et r, et surtout χ. C’est ce que nous avons fait dans le formulaire, où γ3 et ω3 sont utilisés une seule fois au départ pour calculer α3, puis recalculés à la fin une fois tous les autres paramètres déterminés.
Si l’on considère maintenant les γi et ωi comme des inconnues et si l’on rajoute un paramètre a0
(en relation directe avec la largeur angulaire maximale), il se rajoute
une quatrième équation de type (1), et l’on obtient un système de 21
équations à 21 inconnues et 10 paramètres. Le choix de ce qui joue le
rôle de paramètre et celui d’inconnue est d’ailleurs totalement
arbitraire : on peut soit tenter de résoudre les équations en fonction
des données mesurées (méthode directe), ou bien attribuer des valeurs
test à des inconnues et calculer quelles devraient alors être les
valeurs mesurées, et les comparer aux mesures effectives, ou bien même
une méthode mixte.
Une nouvelle méthode de calcul :
Il s’avère que cette dernière méthode est la plus efficace et facile
à mettre en œuvre : nous posons comme valeurs test les azimuts βi et les aplatissements ri, ainsi que la largeur angulaire maximale 2ε0, ce qui permet de calculer tous les autres paramètres angulaires ou dimensionnels. Le choix des βi comme valeurs de test vient de ce que cela conduit à une moindre sensibilité aux variations.
La procédure est la suivante : (2) fournit αi en fonction de α0 et βi ; χ étant fonction de α1, α2, βi et β2, χ est fonction de α0, β1 et β2 ; par inversion, α0 est fonction de χ, β1 et β2, et donc αi est fonction de χ et des βk. (3) fournit γi en fonction de χ et des βk. L’inversion de (6) fournit Ωi en fonction de χ, ri et des βk. (5) fournit ωi en fonction de χ, ri et des βk.
On peut contrôler que (4) est bien vérifiée, preuve que les équations
étaient dépendantes et qu’on ne pouvait pas attribuer des valeurs
mesurées quelconques à la fois à r, γi et ωi. Le paramètre ε0 permet enfin avec (1) de trouver ai en fonction de ε0, χ et des βk (et bien sûr de la distance focale f), puis de trouver bi en fonction de ε0, χ et des βk.
La simple donnée de valeurs test pour les βi permet donc de déduire les αi et les γi ; la donnée de valeurs mesurées et corrigées pour les ri permet de déduire les Ωi et les ωi ; la donnée d’une valeur test pour ε0 permet de déduire les ai et les bi.
Le jeu de test permet aussi de calculer la position du nuage et de
l’horizon sur la photo 4 et donc de le valider ou non. Il faut ensuite
que les valeurs trouvées pour γ–ω soient compatibles avec celles mesurées sur les photos 3 et 4 où la mesure est fiable, et que les valeurs a et b soient cohérentes avec celles mesurées après correction de distorsion.
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:54
VII - Un trucage photographique ?
Introduction : Galerie de photos Chauvet
Voici tout d'abord
quelques scans tirés des copies originales de seconde génération
prêtées par Laurent Guérin. Malgré la compression jpeg, elles sont
quand même de bien meilleure qualité que les images que j'avais
publiées jusqu'à lors sur mon site (voir chapitre I), et qui étaient
tirées du livre de Pierre Guérin.
L'agrandissement de l'objet sur la
photo 3 en particulier est je trouve assez impressionnant. Il est
effectivement très net, comme "découpé au couteau" (dixit Pierre
Guérin), et la bande sombre est bien visible.
Cliquez sur les photos pour les voir en plein écran.

Le trucage photographique est aussi vieux que l'invention de la
photographie, et l'ufologie n'y a pas échappé. La plupart des
techniques de trucage étaient déjà au point dès les années 20/30, et il
a fallu attendre l'explosion de la micro-informatique, et des logiciels
grand public (tel Photoshop) dans les années 90 pour franchir une
nouvelle étape qualitative : celle du numérique.
Truquer une photo
est possible, même souvent pour un simple amateur averti. Les
sceptiques en concluent donc, à tort, qu'on ne peut accorder aucune
valeur (ni preuve, ni indice) à quelque photo d'ovni que ce soit. Les
"croyants" ont eux le défaut inverse, celui de s'enthousiasmer
instantanément et sans aucun esprit critique pour le premier cliché
flou venu, et à persister dans leur croyance même lorsque des experts
l'ont estimé plus que douteux.
Truquer une photo est possible donc,
mais pas toujours facile. Le "crime parfait" est plus rare qu'on ne le
dit, il y a toujours un détail qui cloche, une anomalie oubliée par le
photographe et qui permet de deviner la fraude. Et en 1952, avant l'ère
du tout-numérique c'était encore bien plus difficile : pas d'assistance
informatique avec de puissants logiciels permettant de retoucher au
pixel près chaque parcelle du cliché, pas de possibilité de réessayer
des centaines de fois jusqu'à obtention du résultat parfait.
Il y a deux grandes manières de détecter un trucage photographique :
dossier Chauvet (notamment II et V) j'ai utilisé la première méthode,
et je pense avoir démontré qu'il n'existe aucune faille, aucune erreur
patente dans ces photos, aucune incohérence avec le témoignage d' André
Frégnale. En particulier les positions de l'objet sont compatibles avec
la trajectoire estimée par le témoin. Et pourtant cette série est
exceptionnellement "riche" en informations (4 photos consécutives,
d'excellente qualité, sur un film et avec un appareil au "top" de
l'époque, prises par un professionnel, avec divers éléments de paysage
visibles.
Dans ce chapitre je vais démontrer de même qu'on ne
détecte aucune trace d'aucun des trucages connus sur cette série de
photos. Mais mieux encore, je vais démontrer pourquoi il n'y avait
aucun moyen de les truquer. L'insertion des 4 photos au sein d'un film anodin
Certains
sceptiques ont cru pouvoir accorder plus de chances au canular, en
imaginant que les 4 photos auraient été faites à bien plus que 8
secondes d'intervalle. M. Frégnale aurait fait plusieurs essais,
attendu d'avoir les conditions idéales, puis aurait déclenché chaque
photo au moment opportun. A la limite plusieurs jours pourraient
séparer chaque cliché
Or il est avéré que sur le négatif original, ces 4 photos étaient précédées et suivies de photos anodines.
Certains
sceptiques ont donc avancé que Frégnale aurait rephotographié les
clichés truqués avec une autre pellicule, commençant par des images
anodines.
Cela lui aurait ainsi laissé tout le temps (peut être
plusieurs jours) pour réaliser plusieurs essais, des dizaines si
nécessaire, puis de sélectionner les quatre meilleurs clichés, pour
enfin les insérer au milieu d'une pellicule ordinaire, et faire croire
au "coup de chance".
Cette hypothèse se heurte aux mêmes objections déjà soulevées à propos d'un éventuel canular (voir chapitres II et V) :
La surimpression à la prise de vue
Aussi appelée "double
exposition", elle consiste à photographier deux fois le même bout de
pellicule, une première fois le paysage seul, puis la seconde fois
l'objet (la "soucoupe" seule). Au tirage les deux apparaissent sur la
même photo.
Cette hypothèse est rejetée d'amblée, à juste titre
par Pierre Guérin, qui a examiné rappelons-le le négatif original au
microscope. Je cite Pierre Guérin, page 121 de son livre "OVNI, les
mécanismes d'une désinformation" :
propres recherches confirment d'ailleurs que l'appareil de Frégnale, un
Contessa pliable 533/24, ne permettait pas mécaniquement le rembobinage
de la pellicule. Le photomontage

Certains sceptiques ont alors imaginé le "trucage photographique
intégral", c'est à dire un photomontage à la colle et aux ciseaux,
l'ancêtre des manipulations d'aujourd'hui avec Photoshop ou
PaintShopPro.
Selon les sceptiques une photo d'ovni n'a strictement
aucune valeur car, avec du temps et de l'expérience on pourrait
réaliser n'importe quel trucage, et le rendre totalement indétectable.
Aujourd'hui
en effet, grâce à l'informatique, quasiment n'importe qui peut réaliser
un photomontage comme celui ci-contre. Eh oui ! Si l'on en juge par
cette photo, Georges Bush sait qu'"ILS" sont là, et a scellé un pacte
avec eux ... brrrr :-).
Pourtant, cette croyance, largement
répandue dans le grand public, tient pour moi largement du mythe, et a
pris son essor avec l'ère du numérique. Dans la pratique les trucages
destinés à tromper le public sont assez rares, et il y a le plus
souvent des moyens assez simples de les repérer, surtout à l'époque de
l'argentique.
Mais faisons d'abord un peu d'historique.
Bref historique du trucage photo
Le photomontage n'est hélas pas qu'un amusement. Il fut même parfois utilisé pour tromper le grand public comme le montre cet épisode, dont voici un extrait : When Bill Clinton shook Cuban leader
Fidel Castro's hand at the United Nations, the New York Daily News was
the only one of the city's major publications to capture the first-ever
meeting between a sitting United States president and Castro.
There was only one catch -- the photo had never been taken.
Instead,
the photo was actually a montage -- a composite photograph of two
pictures that were combined to illustrate a moment that reporters had
witnessed but photographers hadn't photographed.
A insi donc,
très récemment, le New York Daily News n'a pas hésité, pour faire un
scoop et augmenter ses ventes, à monter de toutes pièces une photo
entre Bill Clinton et Fidel Castro.
Encore plus "sombre" : le
photomontage politique. Tout le monde sait (ou devrait savoir),
qu'après chaque purge, Staline faisait effacer, par simple retouche des
photos officielles, les personnages, jadis hauts dignitaires du régime,
et qu'il avait fait arrêter puis assassiner.
Heureusement ces cas sont rares.
Venons-en maintenant aux trucages utilisés en ufologie, depuis 1947.
Le trucage photo en ufologie
Introduction : Galerie de photos Chauvet
Voici tout d'abord
quelques scans tirés des copies originales de seconde génération
prêtées par Laurent Guérin. Malgré la compression jpeg, elles sont
quand même de bien meilleure qualité que les images que j'avais
publiées jusqu'à lors sur mon site (voir chapitre I), et qui étaient
tirées du livre de Pierre Guérin.
L'agrandissement de l'objet sur la
photo 3 en particulier est je trouve assez impressionnant. Il est
effectivement très net, comme "découpé au couteau" (dixit Pierre
Guérin), et la bande sombre est bien visible.
Cliquez sur les photos pour les voir en plein écran.
| Photo intégrale | Commentaire | Zoom sur l'objet |

Le trucage photographique est aussi vieux que l'invention de la
photographie, et l'ufologie n'y a pas échappé. La plupart des
techniques de trucage étaient déjà au point dès les années 20/30, et il
a fallu attendre l'explosion de la micro-informatique, et des logiciels
grand public (tel Photoshop) dans les années 90 pour franchir une
nouvelle étape qualitative : celle du numérique.
Truquer une photo
est possible, même souvent pour un simple amateur averti. Les
sceptiques en concluent donc, à tort, qu'on ne peut accorder aucune
valeur (ni preuve, ni indice) à quelque photo d'ovni que ce soit. Les
"croyants" ont eux le défaut inverse, celui de s'enthousiasmer
instantanément et sans aucun esprit critique pour le premier cliché
flou venu, et à persister dans leur croyance même lorsque des experts
l'ont estimé plus que douteux.
Truquer une photo est possible donc,
mais pas toujours facile. Le "crime parfait" est plus rare qu'on ne le
dit, il y a toujours un détail qui cloche, une anomalie oubliée par le
photographe et qui permet de deviner la fraude. Et en 1952, avant l'ère
du tout-numérique c'était encore bien plus difficile : pas d'assistance
informatique avec de puissants logiciels permettant de retoucher au
pixel près chaque parcelle du cliché, pas de possibilité de réessayer
des centaines de fois jusqu'à obtention du résultat parfait.
Il y a deux grandes manières de détecter un trucage photographique :
- détecter une incohérence, une anomalie intrinsèque à l'image, et ceci indépendamment de la technique de prise de vue utilisée.
- détecter une trace du type de trucage utilisé, une
imperfection, un résidu quelconque. Par exemple une nette
sous-exposition de la "soucoupe" trahit généralement une technique de
"double-exposition".
dossier Chauvet (notamment II et V) j'ai utilisé la première méthode,
et je pense avoir démontré qu'il n'existe aucune faille, aucune erreur
patente dans ces photos, aucune incohérence avec le témoignage d' André
Frégnale. En particulier les positions de l'objet sont compatibles avec
la trajectoire estimée par le témoin. Et pourtant cette série est
exceptionnellement "riche" en informations (4 photos consécutives,
d'excellente qualité, sur un film et avec un appareil au "top" de
l'époque, prises par un professionnel, avec divers éléments de paysage
visibles.
Dans ce chapitre je vais démontrer de même qu'on ne
détecte aucune trace d'aucun des trucages connus sur cette série de
photos. Mais mieux encore, je vais démontrer pourquoi il n'y avait
aucun moyen de les truquer. L'insertion des 4 photos au sein d'un film anodin
Certains
sceptiques ont cru pouvoir accorder plus de chances au canular, en
imaginant que les 4 photos auraient été faites à bien plus que 8
secondes d'intervalle. M. Frégnale aurait fait plusieurs essais,
attendu d'avoir les conditions idéales, puis aurait déclenché chaque
photo au moment opportun. A la limite plusieurs jours pourraient
séparer chaque cliché
Or il est avéré que sur le négatif original, ces 4 photos étaient précédées et suivies de photos anodines.
Certains
sceptiques ont donc avancé que Frégnale aurait rephotographié les
clichés truqués avec une autre pellicule, commençant par des images
anodines.
Cela lui aurait ainsi laissé tout le temps (peut être
plusieurs jours) pour réaliser plusieurs essais, des dizaines si
nécessaire, puis de sélectionner les quatre meilleurs clichés, pour
enfin les insérer au milieu d'une pellicule ordinaire, et faire croire
au "coup de chance".
Cette hypothèse se heurte aux mêmes objections déjà soulevées à propos d'un éventuel canular (voir chapitres II et V) :
- Le canular de type frisbee ou maquette suspendue est techniquement impossible.
- André Frégnale n'avait aucun mobile. Il n'a tiré strictement
aucun profit de ce canular, et ne l'a jamais reconnu. Quant à la
motivation par l'envie de se payer la tête des autorités ou des
"savants", et par dépit de ne pas être reconnu à sa juste valeur, elle
reste entièrement à démontrer. - Un tel canular aurait nécessité au moins un complice, alors
qu'André Frégnale était un solitaire. Un tel complice n'aurait-il pas
parlé un jour ?
La surimpression à la prise de vue
Aussi appelée "double
exposition", elle consiste à photographier deux fois le même bout de
pellicule, une première fois le paysage seul, puis la seconde fois
l'objet (la "soucoupe" seule). Au tirage les deux apparaissent sur la
même photo.
Cette hypothèse est rejetée d'amblée, à juste titre
par Pierre Guérin, qui a examiné rappelons-le le négatif original au
microscope. Je cite Pierre Guérin, page 121 de son livre "OVNI, les
mécanismes d'une désinformation" :
"D'autre part, ces images ne pouvaient pas résulterMes
d'une surimpression par le biais d'une glace sans tain ou de tout autre
procédé comme la double exposition (au demeurant, impossible à réaliser
avec l'appareil photo du témoin), car un tel artifice n'aurait pu
laisser sous-exposée la face inférieure sombre de la soucoupe sur
laquelle se serait imprimé le fond clair du ciel. Les photos montraient
donc un objet dans le ciel lui-même, mais quel objet ?"
propres recherches confirment d'ailleurs que l'appareil de Frégnale, un
Contessa pliable 533/24, ne permettait pas mécaniquement le rembobinage
de la pellicule. Le photomontage

Certains sceptiques ont alors imaginé le "trucage photographique
intégral", c'est à dire un photomontage à la colle et aux ciseaux,
l'ancêtre des manipulations d'aujourd'hui avec Photoshop ou
PaintShopPro.
Selon les sceptiques une photo d'ovni n'a strictement
aucune valeur car, avec du temps et de l'expérience on pourrait
réaliser n'importe quel trucage, et le rendre totalement indétectable.
Aujourd'hui
en effet, grâce à l'informatique, quasiment n'importe qui peut réaliser
un photomontage comme celui ci-contre. Eh oui ! Si l'on en juge par
cette photo, Georges Bush sait qu'"ILS" sont là, et a scellé un pacte
avec eux ... brrrr :-).
Pourtant, cette croyance, largement
répandue dans le grand public, tient pour moi largement du mythe, et a
pris son essor avec l'ère du numérique. Dans la pratique les trucages
destinés à tromper le public sont assez rares, et il y a le plus
souvent des moyens assez simples de les repérer, surtout à l'époque de
l'argentique.
Mais faisons d'abord un peu d'historique.
Bref historique du trucage photo
 | Dès le XIXème siècle, les artistes ont exploré toutes les possibilités de ce mouveau media qu'est la photographie, et ils n'ont pas cessé depuis. La photo de gauche date de 1902, celle de droite - beaucoup plus récente - est signé Newry, l'un des artistes actuels les plus côtés sur ce type d'oeuvre. Sur cet excellent site, dédié au "Cut&Paste", on peut lire notamment : "A variety of methods for making composite photographs was discovered during the Victorian era. The more complex examples were constructed in the darkroom using multiple exposures onto the same plate, with unexposed areas being masked by pieces of black velvet, presaging the precise realism of the likes of John Heartfield, who employed professional photographers to seamlessly blend his ideas in the darkroom. Other images were produced from a more primitive "cut and paste" technique, and the final picture then rephotographed, an approach to montage that has persisted ever since, and still finds favour with some of today's montage artists like Sean Hillen." |  |
Fidel Castro's hand at the United Nations, the New York Daily News was
the only one of the city's major publications to capture the first-ever
meeting between a sitting United States president and Castro.
There was only one catch -- the photo had never been taken.
Instead,
the photo was actually a montage -- a composite photograph of two
pictures that were combined to illustrate a moment that reporters had
witnessed but photographers hadn't photographed.
A insi donc,
très récemment, le New York Daily News n'a pas hésité, pour faire un
scoop et augmenter ses ventes, à monter de toutes pièces une photo
entre Bill Clinton et Fidel Castro.
Encore plus "sombre" : le
photomontage politique. Tout le monde sait (ou devrait savoir),
qu'après chaque purge, Staline faisait effacer, par simple retouche des
photos officielles, les personnages, jadis hauts dignitaires du régime,
et qu'il avait fait arrêter puis assassiner.
Heureusement ces cas sont rares.
Venons-en maintenant aux trucages utilisés en ufologie, depuis 1947.
Le trucage photo en ufologie
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:54
Comme le rappelle ce site, les méthodes de trucage étaient relativement peu nombreuses et assez frustres :
Primitive ways of faking UFO photos —
before modern computers — included throwing objects in the air (such as
trashcan lids, breakfast bowls, hats, or ordinary dinner plates) and
photographing them against whatever scenery you thought would look
good. It was usually best to get the object against a clear part of the
sky so that its size could not be easily measured.
Another method was simply to draw, paint, or paste a disk or cigar-shaped object on to a picture and then photograph it again. The new picture would be a little more blurred than the original, and would look more realistic and less detectable as a fake.
N B : les emphases en gras sont de moi.
La
première technique citée ici, et la plus largement utilisée, consistait
donc à lancer un objet en l'air, ou bien à le suspendre par un fil
invisible à une haute branche ou à un fil électrique quelconque. Cet
objet étant bien entendu une maquette de "soucoupe" de petite taille
(moins de 50 cm), ou plus fréquemment un objet courant détourné de sa
fonction première pour faire illusion (enjoliveur, moule à tarte,
rétroviseur de camion, ...)
Voici comme illustration de ce procédé les célèbres photos truquées du "contacté" Suisse Billy Meier :


Cette
technique n'a pas pu être utilisée pour Chauvet, comme je l'ai démontré
au chapitre II et comme Pierre Guérin l'avait lui même affirmé dans son
livre. D'ailleurs aucun sceptique interrogé sur ce cas n'a contesté
cela. C'était pourtant la technique de trucage largement majoritaire en
ufologie à cette époque, et de loin.
La seconde technique est
celle du photomontage proprement dit, que nous allons aborder
pleinement dans les sections suivantes. Mais il faut commencer par
noter que le disque de Chauvet n'est pas flou ("blurred") du tout, au
moins sur les photos 3 et 4, ce qui tendrait déjà à nous rendre
sceptique sur l'emploi de ce trucage. Principe du photomontage
Le principe du photomontage appliqué au cas Chauvet
J'ai
contacté plusieurs photographes professionnels ou amateurs avertis, en
personne ou via des forums de discussion, ou via leurs sites web. Aucun
n'a réellement voulu "se mouiller" quant à savoir si les photos Chauvet
ont pu être fabriquées par photomontage. Ils m'ont tous raconté des
techniques de trucage, certes efficaces et sur un ton visiblement
passionné et expert, mais qui ne s'appliquaient pas en l'occurence au
cas Chauvet (utilisation d'informatique, de films spéciaux qui
n'existaient pas en 1952, etc.).
Certes, la plupart d'entre eux
(mais pas tous), finissait par dire, lorsque je les poussais dans leurs
derniers retranchements, qu'à leur avis, ces photos avaient pu être
truquées, car "en photo on peut tout faire". Ils reproduisaient en cela
le mythe populaire dont j'ai parlé plus haut. Mais en pratique, aucun
n'a pu m'expliquer à ce jour en détail comment techniquement ce trucage
avait été réalisé (NDR : cette page est donc implicitement un appel
=> si un photographe expert, lecteur de mon site, sait comment
Frégnale a pu faire, qu'il m'écrive !).
Une de mes
relations, scientifique à Orsay, Joël E., fut dès le début adepte de la
thèse du trucage. Il a consulté un photographe de ses connaissances qui
lui a confirmé que les photos Chauvet auraient bien pu être réalisées
par photomontage. Hélas, ce photographe lui aussi préfère apparemment
l'anonymat, et je n'ai pas encore eu la possibilité de l'interviewer
directement, afin d'obtenir de sa bouche ses explications techniques
adaptées au contexte Chauvet, ou les fameux "nombreux exemples" de
trucages similaires qui - prétend-t-il - étaient réalisés à l'époque.
J'espère que Joël pourra m'obtenir cette faveur :-)
Mais, selon ce que m'en a rapporté Joël, le trucage aurait consisté grossièrement à :
tel montage demande une grande rigueur pour ne pas introduire
d'invraisemblance, et il faut avant tout faire des croquis du résultat
recherché pour déterminer tous les paramètres des prises de vue. Pour
la bande noire sous la soucoupe, il suffit de peindre la maquette
conformément au croquis préalable. La photo de la maquette peut se
faire en intérieur avec éclairage artificiel, car la luminosité de
l'objet peut être arbitraire (dans certaines limites de vraisemblance),
et il n'est pas nécessaire de la suspendre bien haut puisque sa taille
sur le négatif n'a pas besoin d'être la même que dans le montage final.
Discussion / Réfutation de la thèse du photomontage
Mais,
malgré quelques précautions de langage ("une grande rigueur de
montage"), cette explication relève encore un peu de la profession de
foi. Elle est trop générale, trop passe-partout. Il faudrait, soit
l'appliquer au cas particulier des photos Chauvet, soit avoir des
exemples de trucages similaires.
A l'appui de cette thèse, Joël citait cet article
de la célèbre photographe Andrée Preschia. Dans son esprit il
illustrait le fait que cette technique du photomontage permettait non
seulement d'effectuer le trucage des photos Chauvet, mais était
également très ancienne et très connue des professionnels.
Pourtant,
à la lecture de cet excellent article, mon opinion est toute autre, et
je ne peux que regretter davantage de ne pouvoir entrer directement en
contact avec sa "source", ou avec tout autre photographe expert sur la
question (de plus en plus rares avec le raz de marée du numérique). En
effet il apparait immédiatement à la lecture de ce texte, plusieurs
objections de fond, qui rendent la thèse du photomontage pour Chauvet,
non seulement invraisemblable, mais carrément impossible techniquement :
Conclusion / Synthèse
Dans le cas Chauvet, cette explication par photomontage est donc invraisemblable:
M. Gervereau : "Les images qui mentent" (2000) - Paris, Seuil (458 pages)
=== Ufologie et photos truquées
Les photos controversées de Gulf Breeze : http://www.virtuallystrange.net/ufo/updates/1999/oct/m16-014.shtml
Galeries de photos d'ovnis : http://thebiggestsecretpict.online.fr/ufo_et.htm
Les photos truquées de Billy Meier : http://www.iigwest.com/ufopix.html
D'autres photos d'ovnis truquées : http://www.users.bigpond.com/rdoolan/ufopicfakes.html :
Dossier "photos d'ovnis (truquées ou pas) : http://studiovni.ifrance.com/studiovni/som013.htm
=== Comment créer de fausses photos d'ovnis :
http://ncas.sawco.com/ufosymposium/p243fake.html (site sceptique)
http://www.garfnet.org.uk/new_mill/bbmedia/issue001/ufo_fake.htm
=== Photomontage artistique
Site dédié au "cut & paste" : http://www.cutandpaste.info/, mais principalement en tant qu'art
Technique du photomontage (Article d'Andrée Freschia)) : http://www.rtfm.be/king/photomontage/index.html
Primitive ways of faking UFO photos —
before modern computers — included throwing objects in the air (such as
trashcan lids, breakfast bowls, hats, or ordinary dinner plates) and
photographing them against whatever scenery you thought would look
good. It was usually best to get the object against a clear part of the
sky so that its size could not be easily measured.
Another method was simply to draw, paint, or paste a disk or cigar-shaped object on to a picture and then photograph it again. The new picture would be a little more blurred than the original, and would look more realistic and less detectable as a fake.
N B : les emphases en gras sont de moi.
La
première technique citée ici, et la plus largement utilisée, consistait
donc à lancer un objet en l'air, ou bien à le suspendre par un fil
invisible à une haute branche ou à un fil électrique quelconque. Cet
objet étant bien entendu une maquette de "soucoupe" de petite taille
(moins de 50 cm), ou plus fréquemment un objet courant détourné de sa
fonction première pour faire illusion (enjoliveur, moule à tarte,
rétroviseur de camion, ...)
Voici comme illustration de ce procédé les célèbres photos truquées du "contacté" Suisse Billy Meier :


Cette
technique n'a pas pu être utilisée pour Chauvet, comme je l'ai démontré
au chapitre II et comme Pierre Guérin l'avait lui même affirmé dans son
livre. D'ailleurs aucun sceptique interrogé sur ce cas n'a contesté
cela. C'était pourtant la technique de trucage largement majoritaire en
ufologie à cette époque, et de loin.
La seconde technique est
celle du photomontage proprement dit, que nous allons aborder
pleinement dans les sections suivantes. Mais il faut commencer par
noter que le disque de Chauvet n'est pas flou ("blurred") du tout, au
moins sur les photos 3 et 4, ce qui tendrait déjà à nous rendre
sceptique sur l'emploi de ce trucage. Principe du photomontage
 | + |  | = |  |
J'ai
contacté plusieurs photographes professionnels ou amateurs avertis, en
personne ou via des forums de discussion, ou via leurs sites web. Aucun
n'a réellement voulu "se mouiller" quant à savoir si les photos Chauvet
ont pu être fabriquées par photomontage. Ils m'ont tous raconté des
techniques de trucage, certes efficaces et sur un ton visiblement
passionné et expert, mais qui ne s'appliquaient pas en l'occurence au
cas Chauvet (utilisation d'informatique, de films spéciaux qui
n'existaient pas en 1952, etc.).
Certes, la plupart d'entre eux
(mais pas tous), finissait par dire, lorsque je les poussais dans leurs
derniers retranchements, qu'à leur avis, ces photos avaient pu être
truquées, car "en photo on peut tout faire". Ils reproduisaient en cela
le mythe populaire dont j'ai parlé plus haut. Mais en pratique, aucun
n'a pu m'expliquer à ce jour en détail comment techniquement ce trucage
avait été réalisé (NDR : cette page est donc implicitement un appel
=> si un photographe expert, lecteur de mon site, sait comment
Frégnale a pu faire, qu'il m'écrive !).
Une de mes
relations, scientifique à Orsay, Joël E., fut dès le début adepte de la
thèse du trucage. Il a consulté un photographe de ses connaissances qui
lui a confirmé que les photos Chauvet auraient bien pu être réalisées
par photomontage. Hélas, ce photographe lui aussi préfère apparemment
l'anonymat, et je n'ai pas encore eu la possibilité de l'interviewer
directement, afin d'obtenir de sa bouche ses explications techniques
adaptées au contexte Chauvet, ou les fameux "nombreux exemples" de
trucages similaires qui - prétend-t-il - étaient réalisés à l'époque.
J'espère que Joël pourra m'obtenir cette faveur :-)
Mais, selon ce que m'en a rapporté Joël, le trucage aurait consisté grossièrement à :
- Prendre 4 photos du paysage sans la soucoupe et en tirer de forts agrandissements (ex : 20x25 à 30x40)
- Prendre 4 photos d'une maquette de soucoupe en labo, sous des
conditions adéquates d'éclairage, et en tirer de forts agrandissements - Découper soigneusement les 4 images de soucoupe et les coller sur les 4 photos agrandies du paysage
- soigneusement maquiller au crayon gras pour effacer toute trace de raccord,
- Rephotographier au banc les images ainsi obtenues sur un film déjà commencé et contenant des clichés anodins
tel montage demande une grande rigueur pour ne pas introduire
d'invraisemblance, et il faut avant tout faire des croquis du résultat
recherché pour déterminer tous les paramètres des prises de vue. Pour
la bande noire sous la soucoupe, il suffit de peindre la maquette
conformément au croquis préalable. La photo de la maquette peut se
faire en intérieur avec éclairage artificiel, car la luminosité de
l'objet peut être arbitraire (dans certaines limites de vraisemblance),
et il n'est pas nécessaire de la suspendre bien haut puisque sa taille
sur le négatif n'a pas besoin d'être la même que dans le montage final.
Discussion / Réfutation de la thèse du photomontage
Mais,
malgré quelques précautions de langage ("une grande rigueur de
montage"), cette explication relève encore un peu de la profession de
foi. Elle est trop générale, trop passe-partout. Il faudrait, soit
l'appliquer au cas particulier des photos Chauvet, soit avoir des
exemples de trucages similaires.
A l'appui de cette thèse, Joël citait cet article
de la célèbre photographe Andrée Preschia. Dans son esprit il
illustrait le fait que cette technique du photomontage permettait non
seulement d'effectuer le trucage des photos Chauvet, mais était
également très ancienne et très connue des professionnels.
Pourtant,
à la lecture de cet excellent article, mon opinion est toute autre, et
je ne peux que regretter davantage de ne pouvoir entrer directement en
contact avec sa "source", ou avec tout autre photographe expert sur la
question (de plus en plus rares avec le raz de marée du numérique). En
effet il apparait immédiatement à la lecture de ce texte, plusieurs
objections de fond, qui rendent la thèse du photomontage pour Chauvet,
non seulement invraisemblable, mais carrément impossible techniquement :
- Comme l'indique clairement Andrée Preschia, le photomontage qu'elle
décrit s'inscrit plutôt dans le courant "artistique / créatif" de la
photographie, et non dans le courant "recherche de ressemblance". Ces
deux courants ont existé dès les débuts de la photographie, et
caractérisent encore aujourd'hui la plupart des professionnels : on est
soit l'un, soit l'autre, rarement les deux. - Je cite : "Toujours avant le collage, il faudra colorer
l'épaisseur du papier découpé. Si le fond sur lequel le sujet doit être
collé est blanc, la tranche étant également blanche, il n'y a rien à
faire. Mais si le sujet doit se coller sur un fond gris ou noir, il est
préférable de teinter l'épaisseur de la même couleur que le fond sur
lequel il va trouver place. Si ce travail n'a pas été fait, à la
reproduction, les sujets risquent d'être entourés d'un fin liseré
blanc."
Comment imaginer, avec les moyens de l'époque, une
retouche aussi fine, qui reste invisible malgré un agrandissement
maximal (c'est à dire qui montre le grain du film) ?? - Il faut ensuite retoucher les images au crayon gras. Même
remarque donc que précédemment. Aux agrandissements réalisés par Pierre
Guérin, comment imaginer que de telles retouches restent invisibles ? - Je cite : "L'image à reproduire doit avoir un format supérieur à celui du tirage définitif. 40/50cm pour un tirage définitif de 30/40". Or les photos ont ensuite été agrandies au maximum possible,
puisqu'on a atteint le grain du film, et l'image du disque est toujours
nette (photos 3 et 4) ! Cela n'aurait pu être possible que si la
rephotographie avait été fait d'après une première épreuve de taille
encore plus grande ... ce qui n'était pas possible (limites du film
24x36). - Enfin, last but not least, je cite : "Le film employé
pour la reproduction aura un grain plus gros que le film d'origine
(pour un 100 ISO, prendre un 200 ou un 400 ISO) De cette façon, le gros
grain masque le grain fin et l'image paraît plus nette.".
Les références exactes du film utilisé par Frégnale sont : Kodak Panatomic-X (5060) FX BW (ISO 32). Où 5060 est le Film Code Number, FX est le Code Name
Ce
film était le plus fin disponible à l'époque, et il a détenu ce record
très longtemps jusqu'à l'arrivée d'abord du Kodak Technical Pan, puis
en 1987 du T-Max 100. La NASA (qui n'existait pas en 1952 !) l'a utilisé, sa version "aerial" est la référence en matière de photo aérienne, il reste très utilisé en photo astronomique, et de nombreux amateurs ne jurent encore aujourd'hui que par lui. Ce film est devenu si fameux, que des plug-ins pour Photoshop, émulant son grain et ses tonalités ont même été développés !
Son
pouvoir de résolution incroyablement fin varie de 180 lpm à 200 lpm
selon les sources (lpm = lines per millimeter). Pour mémoire, le "top"
actuel, le Kodak Technical Pan, atteint 250 lpm à 300 lpm (selon les
sources), ce qui est un progrès relativement modeste en plus de 50 ans.
Bref,
il n'existait en 1952 aucun film à grain plus fin (< ISO 32) que le
Panatomic-X, qui aurait pu être employé par Frégnale pour prendre les
photos "à retoucher/coller".
Conclusion / Synthèse
Dans le cas Chauvet, cette explication par photomontage est donc invraisemblable:
- Ce genre de trucages n'était pas employé avant l'ère du numérique,
justement en raison de sa difficulté technique. Seuls les artistes
utilisèrent régulièrement le "cut&paste", mais évidemment sans le
souci de devoir faire un trucage invisible, indétectable. Souvent même
le caractère apparent du montage ne donnait que plus de valeur à
l'oeuvre. A l'époque (1952) les seules techniques utilisées pour
truquer des photos d'ovnis étaient bien plus frustres : la maquette
suspendue au bout d'un fil de pêche, ou lancée en l'air comme un
frisbee.
Malgré mes recherches, je n'ai pu trouver à ce jour aucun
exemple de trucage à base de photomontage tel que celui envisagé pour
Chauvet. Si un lecteur en connait un, qu'il me contacte. - Le flouté des deux premieres photos, du à un "bougé" de l'opérateur.
Il aurait d'abord fallu que Frégnale reproduise, à main levée, un
mouvement similaire (vitesse, durée, direction) à la fois sur la photo
du paysage et sur celle de la soucoupe. Mais surtout cela rend
quasi-impossible pour moi tout "raccord" de l'objet découpé avec le
paysage. Avec un objet dont le bord est parfaitement net (comme sur les
photos 3 et 4) on imagine aisément qu'un truqueur ait découpé
soigneusement au cutter selon ce même bord. Mais avec un bord aussi
flou que sur les photos 1 et 2, où diable peut-on découper sans que
cela ne se voit ? - l'orientation de la bande sombre sous la soucoupe, qui suit exactement le sens de la trajectoire
(trajectoire supposée, s'il s'agit d'un canular) : cela complique quand
même sacrément le trucage ! Pourquoi avoir ajouté cette "fioriture"
inutile ... à supposer qu'elle soit réalisable par trucage ? - Quitte à truquer, pourquoi faire une soucoupe qui se "traine" lamentablement à 170 km/h,
moins vite qu'un avion de l'époque ? Pourquoi ne pas avoir décrit par
exemple un brusque virage à 90° et une accélération foudroyante qui
aurait fait disparaitre la soucoupe de sa vue instantanément. Bref,
pourquoi avoir insisté sur un comportement aussi peu étrange, alors que
l'irruption des soucoupes depuis 1947 avait justement surpris les
témoins, et fait la une des journaix, avec leurs performances en vol
"impossibles" ?
- Il aurait fallu des clichés originaux tirés dans un format supérieur au format maximum possible avec un film 24x36, puisque l'objet reste parfaitement net même sur un agrandissement maximal.
- Le Panatomic-X était le film ayant le grain le plus fin en 1952,
il était donc impossible à Frégnale de prendre les clichés non
retouchés originaux avec un film ayant un grain encore plus fin.
M. Gervereau : "Les images qui mentent" (2000) - Paris, Seuil (458 pages)
=== Ufologie et photos truquées
Les photos controversées de Gulf Breeze : http://www.virtuallystrange.net/ufo/updates/1999/oct/m16-014.shtml
Galeries de photos d'ovnis : http://thebiggestsecretpict.online.fr/ufo_et.htm
Les photos truquées de Billy Meier : http://www.iigwest.com/ufopix.html
D'autres photos d'ovnis truquées : http://www.users.bigpond.com/rdoolan/ufopicfakes.html :
Dossier "photos d'ovnis (truquées ou pas) : http://studiovni.ifrance.com/studiovni/som013.htm
=== Comment créer de fausses photos d'ovnis :
http://ncas.sawco.com/ufosymposium/p243fake.html (site sceptique)
http://www.garfnet.org.uk/new_mill/bbmedia/issue001/ufo_fake.htm
=== Photomontage artistique
Site dédié au "cut & paste" : http://www.cutandpaste.info/, mais principalement en tant qu'art
Technique du photomontage (Article d'Andrée Freschia)) : http://www.rtfm.be/king/photomontage/index.html
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
 Benjamin.dResponsable du forum
Benjamin.dResponsable du forum

 Age : 46
Age : 46
Nombre de messages : 12825
Inscription : 11/03/2007
Localisation : France
Emploi : Privé
Passions : Ufologie, Histoire, lecture
Règlement : Règlement
Points de Participation : 21493
 Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Re: (1952) Lac Chauvet, France, Puy-de-Dôme
Jeu 29 Mai 2008, 12:56
VIII : Nouvelles réponses aux sceptiques
Depuis un an je considère avoir accumulé suffisamment
de pièces dans le dossier Chauvet pour que la charge de la
preuve soit inversée : s'il s'agit d'un objet/artefact ou
phénomène connu de l'homme, à charge désormais pour ceux qui
pensent cela de dire lequel, et d'argumenter.
Je reste donc à l'écoute des "sceptiques". Je constate
cependant à leur propos que mon préambule au chapitre V
reste plus
que jamais valable un an après sa publication :
Anecdotiquement, j'ai remarqué à cette occasion,
que tous les sceptiques sont tous immédiatement certains qu'il
ne
s'agit pas d'un "vrai" ovni ... mais tous pour des raisons
différentes et incompatibles entre elles ! Et pour chacun d'eux,
il apparait comme "évident" que son explication
(généralement imaginée très vite, et en
n'ayant qu'une connaissance
superficielle du dossier), est la seule bonne. Or par
définition toutes ces explications sont fausses, sauf au plus une (si j'ai
tort). Cela ne peut que nous amener à relativiser la
confiance que nous pouvons mettre dans nos "certitudes", nos
"premières impressions", et notre "bon sens". Seule à mon
avis une étude approfondie, méthodique et objective des
faits
du dossier, ainsi que la recherche tenace d'éléments
nouveaux et authentiques, peut permettre d'avancer utilement dans
ce genre d'affaires.
En l'occurence m'ont été successivement fournies à ce jour comme "hautement probables" les explications
suivantes :
Est-il besoin de préciser qu'aucune de ces explications ne tient
la route selon moi. J'ai déjà donné pas mal
d'arguments dans mes chapitres précédents. Je vais
néanmoins y revenir ici, puisque de nouvelles hypothèses
surgissent, ou renaissent.
Attention : cette page comporte de très nombreuses illustrations. Son temps de chargement pourra donc être un peu long.
Julien Arlandis
Un enquêteur motivé et perspicace
Jeune informaticien venu récemment à l'ufologie,
de tendance nettement sceptique, julien Arlandis m'a contacté
via mon site, dont l'adresse lui avait été donné
sur le forum Google Francom.ovni. De décembre 2003 à ce
jour nous avons
échangé de nombreux et longs mails sur ce cas, arguments
contre
arguments, avec conviction, mais sans agressivité ni ad hominem, chose
importante à souligner.
Julien s'est passionné et fortement impliqué sur
le cas Chauvet, avec l'aide parfois d'un
sceptique bien connu Dominique Caudron (dit "Oncle Dom"), et il a
porté le sujet sur deux listes de discussion (Francom.ovni et
Aleph).
Il m'a transmis les références d'un petit film sonore N&B des actualités Pathé de 1952,
découvert par Dominique Caudron, tourné très
probablement lors de la reconstitution organisée une semaine
après l'observation par La Montagne, et que j'avais
mentionné aussitôt sur mon site en juin 2004. On y voit
André
Frégnale montrant la trajectoire de l'objet dans le ciel,
commentant ses photos, et lachant un ballon sonde témoin. Le
commentaire audio précise que "les 4 clichés
réalisés ont été soumis à des
experts qui en ont reconnus l'authenticité". Sans doute
s'agit-il des experts du Ministère de l'air que mentionnait La
Montagne (Cf. chapitre IV). J'ai fait plusieurs démarches
auprès du Ministère de la Défense pour retrouver
ses archives, hélas sans succès à ce jour.
En se basant sur le paysage typique entraperçu sur ce film
(voir photo N°5 ci-dessus), et après être allé
sur place, Julien a même
retrouvé le lieu exact de l'observation, qu'il pense
situé à environ 1
km à l'est du lac Chauvet, au sommet d'une colline (le point
rouge à droite du lac Chauvet sur la carte ci-dessous).

Un grand merci donc à Julien Arlandis pour tout cela. Pour le
reste, Julien prend des points de vue assez divergents des miens.
Réfutation des calculs de Guérin
Julien
Arlandis (avec l'aide appuyée mais discrète de Dominique
Caudron) conteste tout d'abord les calculs de Guérin père
et fils, qui démontrent que les 4 photos sont compatibles avec
les déclarations du témoin (trajectoire rectiligne
uniforme, temps de parcours). Il s'en est notamment longuement
ouvert sur la liste Aleph (www.liste-aleph.org).
Comme on peut le voir sur cette page : http://juliendusud.free.fr/trigo.htm,
il prétend que, s'il existe bien des valeurs des
paramètres pour lesquelles l'"anomalie du nuage" disparait, ces
valeurs "corrigées" par laurent Guérin aboutiraient
à des coordonnées différentes de près de
6° entre les deux jeux d'équations. Autrement dit que ces
valeurs ne vérifieraient plus alors le modèle
géométrique de trajectoire postulé par
Guérin (trajectoire rectiligne uniforme).
Pour Julien, ce qu'il faut remettre en cause alors ce n'est pas le
modèle de Guérin, mais le témoignage de
Frégnale.
Malgré plusieurs échanges entre nous, je ne suis pas
parvenu à le convaincre qu'il n'y a pas d'anomalie dans les calculs de Laurent Guérin. L'explication en est
pourtant donnée à la fin du chapitre VI . Reprécisons là néanmoins brièvement ici :
a) Il est normal que les deux façons de calculer conduisent
à des valeurs différentes, c'est lié au fait que
les formules sont dépendantes entre elles et que les valeurs r,
gamma et omega ne peuvent être mesurées
indépendantes. Comme l'incertitude des mesures est forte, la
mesure de deux valeurs entraîne le calcul la troisième. Si
nous disposions de photos où la mesure de r, gamma et omega soit
indiscutable et très précise, et si les deux formules
conduisaient à des valeurs différentes, alors là
oui, cela voudrait dire que le modèle n'est pas
vérifié rigoureusement.
Hélas, contrairement aux grand axes et petits axes
(aisément mesurables), gamma-i n'est pas une valeur
intangible donnée une fois pour toutes par la mesure. Elle est
entâchée d'une grosse incertitude de mesure. Il faut s'en
approcher par approximations successives. C'est justement là
l'un des points clés : La
différence de beta en fonction de (2) ou (3) ne met pas en
défaut le modèle, il met en défaut le choix d'un
triplet de valeurs de mesure de r, gamma et omega dans leur intervalle
d'incertitude, car ces valeurs sont liées et non
indépendantes.
b) D'autre part le problème est surdéterminé : on a 6
équations reliant les variables a, r, alpha, beta, gamma, omega,
OMEGA, soit 7 variables : on ne peut leur faire prendre n'importe
quelle valeur. C'est pour cela que dans le formulaire,
on recalcule gamma et omega et qu'on trouve des valeurs
différentes (en fait sin(gamma)/sin(gamma-omega) reste constant)
entre les valeurs initiales et celles recalculées).
c) Julien a également commis deux erreurs de calcul :
C'est donc tout à fait normal d'arriver à des valeurs
différentes, puisqu'on opère pas les même choix
d'enchaînement de formules dans la
surdétermination.
De plus le modèle initial retenu par Pierre Guérin
était simpliste : trajectoire rectiligne uniforme, objet stable.
Mais de nombreuses variantes sont possibles à imaginer qui, sans
entrer en conflit avec le témoignage, modifieraient
substantiellement les calculs ... et les compliqueraient. Par exemple
si la trajectoire était montante ou descendante de 2 ou 3
degrés ou même alternativement montante et descendante de
ces angles, ou si la normale à l'objet n'était pas
perpendiculaire à la trajectoire mais à 86° (donc une
inclinaison plus complexe que le simple grand omega), ou encore
n'importe quelle légère variation par rapport à
notre trajectoire idéale, il est évident que le
témoin ne s'en serait pas rendu compte, toutes les formules sont
à revoir et permettent des variations de forme suffisamment
souples tant en angles qu'en dimensions pour faire caler l'image
théorique sur la photo.
Julien persiste enfin à réclamer un scan de haute
qualité des originaux (que je n'ai pas), afin dit-il d'affiner
les mesures, et lever les incertitudes notamment sur le calcul de
χ. Alors que c'est inutile, les scans actuels sont de
résolution suffisantes pour cela, et la marge d'incertitude sur
χ est très faible. La distorsion géométrique a
elle aussi bien été prise en compte dans les calculs
(corrections minimes).
La recherche opiniatre d'une explication "normale"
Julien
Arlandis a d'autre part émis successivement différentes
hypothèses censées expliquer ce cas, à chaque fois
en y croyant très fort, et en les trouvant "évidentes"
(avant de passer à une autre) :
L'explication par la "maquette volante"
Julien
a retrouvé la trace d'un certain Weinstein, qui acquit une
courte notoriété en 1952 en construisant et en faisant
voler une maquette de soucoupe volante à hélice
appelée "la chose", propulsée par un petit moteur
thermique d'à peine 5 cc. Ce Weinstein était même un voisin de Frégnale,
puisqu'il habitait Vichy. Il a donc probablement construit cette
"chose" juste après l'observation médiatisée de
Frégnale pour concilier sa passion du modélisme avec
l'actualité exotique du moment. En
témoigne cette page du magazine RADAR du 10 août 1952
(dont j'ai acheté un exemplaire en bon état), soit moins
d'un mois après l'observation du lac Chauvet (cliquer pour
agrandir). A noter que les superstructures (axe de l'hélice /
moteur) sont nettement visibles et reconnaissables sous l'engin.
Cette même année 1952 les modèles en forme de
soucoupe semblaient être à la mode. Julien Arlandis a en effet trouvé
un petit film extrait des actualités Pathé-Gaumont de septembre 52, et montrant une
autre soucoupe, celle d'un certain Agostini. Elle est visiblement en
mode "vol circulaire" (le plus courant à l'époque), et le commentaire
audio d'époque précise qu'elle vole à 150 km/h (ce chiffre a une importance pour la suite).
A noter que, si la dérive arrière (inutile en vol
circulaire) et l'axe hélice / moteur (intégré dans
l'aile) ne sont pas visibles, en
revanche l'énorme train d'atterrissage l'est ! Et c'est normal :
lorsqu'on a passé autant d'heures de travail méticuleux
à monter un tel engin, on n'a pas envie de risquer de le casser
bêtement à la fin de son vol (une arrivée en
douceur sur une longue distance et une pente faible n'est
évidemment pas possible en vol circulaire).
Ce type de
"récréation" existe encore. Des
aéromodélistes s'amusent encore de nos jours
à faire voler "pour le fun" des tas d'objets improbables : fers
à repasser (en balsa !), baignoires, sorcières sur leur
balai, et ... soucoupes volantes ! A noter toutefois que, comme pour la
soucoupe Weinstein, l'axe moteur - hélice est toujours visible
sous l'engin, voire même parfois la dérive arrière.
Réfutation :
Mais en réalité, aussi séduisante et instructive
que soit cette hypothèse, elle n'est pas plausible dans le cas
de l'ovni de Chauvet.
Depuis un an je considère avoir accumulé suffisamment
de pièces dans le dossier Chauvet pour que la charge de la
preuve soit inversée : s'il s'agit d'un objet/artefact ou
phénomène connu de l'homme, à charge désormais pour ceux qui
pensent cela de dire lequel, et d'argumenter.
Je reste donc à l'écoute des "sceptiques". Je constate
cependant à leur propos que mon préambule au chapitre V
reste plus
que jamais valable un an après sa publication :
Anecdotiquement, j'ai remarqué à cette occasion,
que tous les sceptiques sont tous immédiatement certains qu'il
ne
s'agit pas d'un "vrai" ovni ... mais tous pour des raisons
différentes et incompatibles entre elles ! Et pour chacun d'eux,
il apparait comme "évident" que son explication
(généralement imaginée très vite, et en
n'ayant qu'une connaissance
superficielle du dossier), est la seule bonne. Or par
définition toutes ces explications sont fausses, sauf au plus une (si j'ai
tort). Cela ne peut que nous amener à relativiser la
confiance que nous pouvons mettre dans nos "certitudes", nos
"premières impressions", et notre "bon sens". Seule à mon
avis une étude approfondie, méthodique et objective des
faits
du dossier, ainsi que la recherche tenace d'éléments
nouveaux et authentiques, peut permettre d'avancer utilement dans
ce genre d'affaires.
En l'occurence m'ont été successivement fournies à ce jour comme "hautement probables" les explications
suivantes :
- Canular : un complice qui se déplace d'Ouest en Est emportant avec lui un ballon
suspendu à fil - Méprise : avec un objet inconnu (peut être un "objet de plage") de 3,5 à 4
mètres emporté par le vent et qui aurait voyagé
jusque là - Canular : objet tournoyant de type frisbee, éventuellement
lancé par un appareil de type ball-trap - Canular : trucage 100% photographique
- Canular : maquette télécommandée en vol
circulaire maniée par un complice
Est-il besoin de préciser qu'aucune de ces explications ne tient
la route selon moi. J'ai déjà donné pas mal
d'arguments dans mes chapitres précédents. Je vais
néanmoins y revenir ici, puisque de nouvelles hypothèses
surgissent, ou renaissent.
Attention : cette page comporte de très nombreuses illustrations. Son temps de chargement pourra donc être un peu long.
Julien Arlandis
Un enquêteur motivé et perspicace
Jeune informaticien venu récemment à l'ufologie,
de tendance nettement sceptique, julien Arlandis m'a contacté
via mon site, dont l'adresse lui avait été donné
sur le forum Google Francom.ovni. De décembre 2003 à ce
jour nous avons
échangé de nombreux et longs mails sur ce cas, arguments
contre
arguments, avec conviction, mais sans agressivité ni ad hominem, chose
importante à souligner.
Julien s'est passionné et fortement impliqué sur
le cas Chauvet, avec l'aide parfois d'un
sceptique bien connu Dominique Caudron (dit "Oncle Dom"), et il a
porté le sujet sur deux listes de discussion (Francom.ovni et
Aleph).
Il m'a transmis les références d'un petit film sonore N&B des actualités Pathé de 1952,
découvert par Dominique Caudron, tourné très
probablement lors de la reconstitution organisée une semaine
après l'observation par La Montagne, et que j'avais
mentionné aussitôt sur mon site en juin 2004. On y voit
André
Frégnale montrant la trajectoire de l'objet dans le ciel,
commentant ses photos, et lachant un ballon sonde témoin. Le
commentaire audio précise que "les 4 clichés
réalisés ont été soumis à des
experts qui en ont reconnus l'authenticité". Sans doute
s'agit-il des experts du Ministère de l'air que mentionnait La
Montagne (Cf. chapitre IV). J'ai fait plusieurs démarches
auprès du Ministère de la Défense pour retrouver
ses archives, hélas sans succès à ce jour.
 - 1 - |  - 2 - |  - 3 - |
 - 4 - |  - 5 - |  - 6 - |
En se basant sur le paysage typique entraperçu sur ce film
(voir photo N°5 ci-dessus), et après être allé
sur place, Julien a même
retrouvé le lieu exact de l'observation, qu'il pense
situé à environ 1
km à l'est du lac Chauvet, au sommet d'une colline (le point
rouge à droite du lac Chauvet sur la carte ci-dessous).
Un grand merci donc à Julien Arlandis pour tout cela. Pour le
reste, Julien prend des points de vue assez divergents des miens.
Réfutation des calculs de Guérin
Julien
Arlandis (avec l'aide appuyée mais discrète de Dominique
Caudron) conteste tout d'abord les calculs de Guérin père
et fils, qui démontrent que les 4 photos sont compatibles avec
les déclarations du témoin (trajectoire rectiligne
uniforme, temps de parcours). Il s'en est notamment longuement
ouvert sur la liste Aleph (www.liste-aleph.org).
Comme on peut le voir sur cette page : http://juliendusud.free.fr/trigo.htm,
il prétend que, s'il existe bien des valeurs des
paramètres pour lesquelles l'"anomalie du nuage" disparait, ces
valeurs "corrigées" par laurent Guérin aboutiraient
à des coordonnées différentes de près de
6° entre les deux jeux d'équations. Autrement dit que ces
valeurs ne vérifieraient plus alors le modèle
géométrique de trajectoire postulé par
Guérin (trajectoire rectiligne uniforme).
Pour Julien, ce qu'il faut remettre en cause alors ce n'est pas le
modèle de Guérin, mais le témoignage de
Frégnale.
Malgré plusieurs échanges entre nous, je ne suis pas
parvenu à le convaincre qu'il n'y a pas d'anomalie dans les calculs de Laurent Guérin. L'explication en est
pourtant donnée à la fin du chapitre VI . Reprécisons là néanmoins brièvement ici :
a) Il est normal que les deux façons de calculer conduisent
à des valeurs différentes, c'est lié au fait que
les formules sont dépendantes entre elles et que les valeurs r,
gamma et omega ne peuvent être mesurées
indépendantes. Comme l'incertitude des mesures est forte, la
mesure de deux valeurs entraîne le calcul la troisième. Si
nous disposions de photos où la mesure de r, gamma et omega soit
indiscutable et très précise, et si les deux formules
conduisaient à des valeurs différentes, alors là
oui, cela voudrait dire que le modèle n'est pas
vérifié rigoureusement.
Hélas, contrairement aux grand axes et petits axes
(aisément mesurables), gamma-i n'est pas une valeur
intangible donnée une fois pour toutes par la mesure. Elle est
entâchée d'une grosse incertitude de mesure. Il faut s'en
approcher par approximations successives. C'est justement là
l'un des points clés : La
différence de beta en fonction de (2) ou (3) ne met pas en
défaut le modèle, il met en défaut le choix d'un
triplet de valeurs de mesure de r, gamma et omega dans leur intervalle
d'incertitude, car ces valeurs sont liées et non
indépendantes.
b) D'autre part le problème est surdéterminé : on a 6
équations reliant les variables a, r, alpha, beta, gamma, omega,
OMEGA, soit 7 variables : on ne peut leur faire prendre n'importe
quelle valeur. C'est pour cela que dans le formulaire,
on recalcule gamma et omega et qu'on trouve des valeurs
différentes (en fait sin(gamma)/sin(gamma-omega) reste constant)
entre les valeurs initiales et celles recalculées).
c) Julien a également commis deux erreurs de calcul :
- Dans son formulaire, il calcule beta à l'aide de gamma
(initial) et alpha (précedemment calculé), alors qu'il
faut calculer beta à partir de alpha et alpha-0, ce dernier
étant calculé auparavant de sorte que khi fasse la valeur
désirée. Puis gamma est recalculé avec alpha et
beta. - il a pris alpha-0 = 47.17° (la valeur dans l'article original), au lieu de celle donnée par le formulaire.
C'est donc tout à fait normal d'arriver à des valeurs
différentes, puisqu'on opère pas les même choix
d'enchaînement de formules dans la
surdétermination.
De plus le modèle initial retenu par Pierre Guérin
était simpliste : trajectoire rectiligne uniforme, objet stable.
Mais de nombreuses variantes sont possibles à imaginer qui, sans
entrer en conflit avec le témoignage, modifieraient
substantiellement les calculs ... et les compliqueraient. Par exemple
si la trajectoire était montante ou descendante de 2 ou 3
degrés ou même alternativement montante et descendante de
ces angles, ou si la normale à l'objet n'était pas
perpendiculaire à la trajectoire mais à 86° (donc une
inclinaison plus complexe que le simple grand omega), ou encore
n'importe quelle légère variation par rapport à
notre trajectoire idéale, il est évident que le
témoin ne s'en serait pas rendu compte, toutes les formules sont
à revoir et permettent des variations de forme suffisamment
souples tant en angles qu'en dimensions pour faire caler l'image
théorique sur la photo.
Julien persiste enfin à réclamer un scan de haute
qualité des originaux (que je n'ai pas), afin dit-il d'affiner
les mesures, et lever les incertitudes notamment sur le calcul de
χ. Alors que c'est inutile, les scans actuels sont de
résolution suffisantes pour cela, et la marge d'incertitude sur
χ est très faible. La distorsion géométrique a
elle aussi bien été prise en compte dans les calculs
(corrections minimes).
La recherche opiniatre d'une explication "normale"
Julien
Arlandis a d'autre part émis successivement différentes
hypothèses censées expliquer ce cas, à chaque fois
en y croyant très fort, et en les trouvant "évidentes"
(avant de passer à une autre) :
- méprise avec un ballon publicitaire échappé de la caravane du tour de France cycliste : abandonnée
- méprise avec un objet inconnu mais banal
emporté par le vent (théorie de Dominique Caudron) :
abandonnée - canular : un complice maniant une maquette discoïdale à hélice et moteur thermique en vol circulaire
- canular (février 2005) : un complice qui se
déplace d'Ouest en Est en tirant un ballon à hélium en forme de soucoupe
L'explication par la "maquette volante"
Julien
a retrouvé la trace d'un certain Weinstein, qui acquit une
courte notoriété en 1952 en construisant et en faisant
voler une maquette de soucoupe volante à hélice
appelée "la chose", propulsée par un petit moteur
thermique d'à peine 5 cc. Ce Weinstein était même un voisin de Frégnale,
puisqu'il habitait Vichy. Il a donc probablement construit cette
"chose" juste après l'observation médiatisée de
Frégnale pour concilier sa passion du modélisme avec
l'actualité exotique du moment. En
témoigne cette page du magazine RADAR du 10 août 1952
(dont j'ai acheté un exemplaire en bon état), soit moins
d'un mois après l'observation du lac Chauvet (cliquer pour
agrandir). A noter que les superstructures (axe de l'hélice /
moteur) sont nettement visibles et reconnaissables sous l'engin.
Cette même année 1952 les modèles en forme de
soucoupe semblaient être à la mode. Julien Arlandis a en effet trouvé
un petit film extrait des actualités Pathé-Gaumont de septembre 52, et montrant une
autre soucoupe, celle d'un certain Agostini. Elle est visiblement en
mode "vol circulaire" (le plus courant à l'époque), et le commentaire
audio d'époque précise qu'elle vole à 150 km/h (ce chiffre a une importance pour la suite).
A noter que, si la dérive arrière (inutile en vol
circulaire) et l'axe hélice / moteur (intégré dans
l'aile) ne sont pas visibles, en
revanche l'énorme train d'atterrissage l'est ! Et c'est normal :
lorsqu'on a passé autant d'heures de travail méticuleux
à monter un tel engin, on n'a pas envie de risquer de le casser
bêtement à la fin de son vol (une arrivée en
douceur sur une longue distance et une pente faible n'est
évidemment pas possible en vol circulaire).
 | La vidéo (format mpeg2, sonore) Attention : 3 MO à télécharger ! ADSL recommandé) Voir la même vidéo en mode "streaming" |  |
Ce type de
"récréation" existe encore. Des
aéromodélistes s'amusent encore de nos jours
à faire voler "pour le fun" des tas d'objets improbables : fers
à repasser (en balsa !), baignoires, sorcières sur leur
balai, et ... soucoupes volantes ! A noter toutefois que, comme pour la
soucoupe Weinstein, l'axe moteur - hélice est toujours visible
sous l'engin, voire même parfois la dérive arrière.
 |  |
Réfutation :
Mais en réalité, aussi séduisante et instructive
que soit cette hypothèse, elle n'est pas plausible dans le cas
de l'ovni de Chauvet.
_______________________________________
Veuillez svp respecter le forum en postant des messages sérieux et constructifs sans SMS. Merci à l'avance et bonne lecture.
Rendez-vous sur le blog Ovni et vie extraterrestre :http://ovni-extraterrestre.com/ Poster votre témoignage: Cliquer ici Perte de mot de passe: cliquer ici
Page 2 sur 3 •  1, 2, 3
1, 2, 3 
 1, 2, 3
1, 2, 3 
- (1952) Les photos du Lac Chauvet, Puy-de-Dôme, France
- Lac Chauvet, l'enquête et l'analyse par IPACO
- Phénomènes connus autour de Laschamps (Puy de Dôme, France).
- 2012: le 08/09 à 4h45 - Dôme (comme une noix) - Esneux (Non précisé)
- 2016: le 10/07 à 12h30 - Une soucoupe volante - Ovnis à le Mont-Dore 63240 - Puy-de-Dôme (dép.63)
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Témoigner
Témoigner