Page 2 sur 5 •  1, 2, 3, 4, 5
1, 2, 3, 4, 5 
 1, 2, 3, 4, 5
1, 2, 3, 4, 5 
 Mathieu.AEquipe du forum
Mathieu.AEquipe du forum

 Age : 40
Age : 40
Nombre de messages : 737
Inscription : 25/05/2009
Localisation : Région varoise
Emploi : Designer Graphique, créateur de sites Web Studio Graphique M42 Animateur Astronomique Professionnel Technicien en aéronautique
Passions : Astronomie, Anthropologie, Spectroscopie, Aéronautique
Règlement : Règlement
Points de Participation : 6866
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mar 25 Nov 2014, 14:44
wacapou a écrit:
Et comme système de propulsion dans le vide.
...
En effet
Mathieu.A a écrit:La MHD fonctionne en présence d'un fluide

_______________________________________
"Tout envisager, ne rien croire" Aimé Michel
 Painde2Equipe du forum
Painde2Equipe du forum

 Age : 54
Age : 54
Nombre de messages : 367
Inscription : 25/06/2012
Localisation : Lorient
Emploi : Contrôleur de travaux finis
Passions : Kinderophiliste
Règlement : Règlement
Points de Participation : 4980
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mar 25 Nov 2014, 18:07
Bonjour à tous
Brrrr, j’ai du aller m’acheter un duvet.
J’ai retrouvé ce document sous une autre présentation :
http://www.3af.fr/article/opinion/le-controle-local-de-la-gravitation-mythe-ou-perspective
Mon interrogation sur l’effet de répulsion est mentionné au point [6] du document.
Je vous joins ci-dessous des images pour l’illustrer :
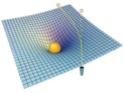
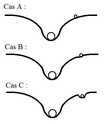
Cas A : la bille magique ne déforme pas le drap (la courbure espace-temps). Sa trajectoire sera courbée.
Cas B : la bille magique déforme légèrement le drap mais ne crée pas de creux. Sa trajectoire sera courbe mais moins que dans le cas A.
Cas C : La bille magique déforme le drap pour former un creux. La trajectoire devient linéaire car la déformation de la boule ne l’influence plus.
Par le biais d’une déformation au point où se trouve la bille magique (hypothèse du document), je ne vois pas comment il peut y avoir une répulsion. Par contre si le point de déformation est légèrement décalé au point de contact de la bille magique, cette dernière peut effectivement se déplacer sans être influencée par la déformation de la boule.
Ai-je bien compris le principe ou doit-on considérer que la déformation de l’espace-temps est décalée à côté de l’objet (bille magique) ?
A+
Brrrr, j’ai du aller m’acheter un duvet.
J’ai retrouvé ce document sous une autre présentation :
http://www.3af.fr/article/opinion/le-controle-local-de-la-gravitation-mythe-ou-perspective
Mon interrogation sur l’effet de répulsion est mentionné au point [6] du document.
Je vous joins ci-dessous des images pour l’illustrer :


Cas A : la bille magique ne déforme pas le drap (la courbure espace-temps). Sa trajectoire sera courbée.
Cas B : la bille magique déforme légèrement le drap mais ne crée pas de creux. Sa trajectoire sera courbe mais moins que dans le cas A.
Cas C : La bille magique déforme le drap pour former un creux. La trajectoire devient linéaire car la déformation de la boule ne l’influence plus.
Par le biais d’une déformation au point où se trouve la bille magique (hypothèse du document), je ne vois pas comment il peut y avoir une répulsion. Par contre si le point de déformation est légèrement décalé au point de contact de la bille magique, cette dernière peut effectivement se déplacer sans être influencée par la déformation de la boule.
Ai-je bien compris le principe ou doit-on considérer que la déformation de l’espace-temps est décalée à côté de l’objet (bille magique) ?
A+
 NycolasEquipe du forum
NycolasEquipe du forum

 Age : 51
Age : 51
Nombre de messages : 716
Inscription : 30/12/2009
Localisation : Saint-Etienne
Emploi : Ecrivain
Passions : Ecriture...
Règlement : Règlement
Points de Participation : 6895
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mar 25 Nov 2014, 18:55
Mathieu.A a écrit:
La MHD fonctionne en présence d'un fluide.
Oui oui, mais peut-être pouvez-vous m'éclairer sur un point, concernant la MHD. J'ai pas mal arpenté le site de JPP, vu un certain nombre de ses conférences, et tout en conservant une distance critique, je suis forcé de constater qu'il sait de quoi il parle. Il y a une chose que je n'ai pas comprise. Je sais que la MHD ne peut pas intervenir dans l'espace pour mouvoir un véhicule, et qu'elle fonctionne par contre dans l'eau. En tout état de cause, elle devrait pouvoir permettre d'ignorer le mur du son, même sous l'eau, or il me semble que JPP dit que ça pose un problème sans en dire plus dans la dernière conférence que j'avais suivie. Si vous avez quelque chose sur ce point précis...
Quoiqu'il en soit, désolé pour cette parenthèse sur la MHD.
Pour ce qui est du sujet en lui-même, je crains qu'il soit très difficile de mener des conjectures sur l'anti-gravitation, dès lors que la gravitation demeure en elle-même un phénomène mesurable et cependant non expliqué... Or si le monde de la physique sèche sur ce point, je crains qu'on n'aille pas non plus bien loin nous-mêmes.
On peut toujours essayer. Pour le moment, je suis assez perplexe sur cette histoire de drap à la Einstein qui se déformerait plus ou moins, plus ou moins en avant, plus ou moins en creux... Cette histoire de répulsion telle que je la comprends correspond à une gravitation négative (si c'est bien ce qu'ils ont voulu dire), tellement négative que la trajectoire de l'objet serait à l'inverse de celle imposée par la gravitation : un objet tendrait à monter vers le ciel au lieu de tomber vers la Terre. Du coup sur un drap, cela voudrait dire que... le drap se courberait à l'inverse et que la bille passerait de l'autre côté ? Hum... Ce drap est décidément gênant pour penser la chose correctement, je trouve. Toute analogie a ses limites, surtout lorsqu'elle force les sens à se faire une représentation concrète de ce qui demeure abstrait.
Il faut aussi envisager que l'anti-gravitation soit plutôt une sorte de gravité multipliée par zéro. Autrement dit un objet employant ce principe ignorerait la gravité comme si elle n'existait pas pour lui (momentanément, peut-être). Et alors on ne peut plus parler d'anti-gravité (l'inverse de la gravité), mais de non-gravité, ou de gravité nulle. Ce qui implique qu'il n'y a plus de drap, et que l'objet ignore tout simplement l'espace-temps. N'oublions pas que ces objets peuvent aussi, apparemment, avoir tendance à disparaitre purement et simplement.
 Mathieu.AEquipe du forum
Mathieu.AEquipe du forum

 Age : 40
Age : 40
Nombre de messages : 737
Inscription : 25/05/2009
Localisation : Région varoise
Emploi : Designer Graphique, créateur de sites Web Studio Graphique M42 Animateur Astronomique Professionnel Technicien en aéronautique
Passions : Astronomie, Anthropologie, Spectroscopie, Aéronautique
Règlement : Règlement
Points de Participation : 6866
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mar 25 Nov 2014, 22:39
Nycolas a écrit:Il y a une chose que je n'ai pas comprise. Je sais que la MHD ne peut pas intervenir dans l'espace pour mouvoir un véhicule, et qu'elle fonctionne par contre dans l'eau. En tout état de cause, elle devrait pouvoir permettre d'ignorer le mur du son, même sous l'eau, or il me semble que JPP dit que ça pose un problème sans en dire plus dans la dernière conférence que j'avais suivie. Si vous avez quelque chose sur ce point précis...
Quoiqu'il en soit, désolé pour cette parenthèse sur la MHD.
A quelle conférence faites vous référence ?
Mathieu
_______________________________________
"Tout envisager, ne rien croire" Aimé Michel
 NycolasEquipe du forum
NycolasEquipe du forum

 Age : 51
Age : 51
Nombre de messages : 716
Inscription : 30/12/2009
Localisation : Saint-Etienne
Emploi : Ecrivain
Passions : Ecriture...
Règlement : Règlement
Points de Participation : 6895
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mar 25 Nov 2014, 23:03
https://www.youtube.com/watch?v=CAmG7_r82-Y
Celle-ci. Elle date un peu, mais le propos de Jean-Pierre sur ce qui se passe sous l'eau n'est pas très clair, et assez bref, je ne sais plus quand... vers le milieu de la conférence, il me semble.
Celle-ci. Elle date un peu, mais le propos de Jean-Pierre sur ce qui se passe sous l'eau n'est pas très clair, et assez bref, je ne sais plus quand... vers le milieu de la conférence, il me semble.
 Mathieu.AEquipe du forum
Mathieu.AEquipe du forum

 Age : 40
Age : 40
Nombre de messages : 737
Inscription : 25/05/2009
Localisation : Région varoise
Emploi : Designer Graphique, créateur de sites Web Studio Graphique M42 Animateur Astronomique Professionnel Technicien en aéronautique
Passions : Astronomie, Anthropologie, Spectroscopie, Aéronautique
Règlement : Règlement
Points de Participation : 6866
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mer 26 Nov 2014, 07:25
Nycolas a écrit:https://www.youtube.com/watch?v=CAmG7_r82-Y
Celle-ci. Elle date un peu, mais le propos de Jean-Pierre sur ce qui se passe sous l'eau n'est pas très clair, et assez bref, je ne sais plus quand... vers le milieu de la conférence, il me semble.
J'avoue ne pas avoir le temps d'écouter l'ensemble de la conférence dans le but de rechercher une phrase ou un bout de phrase en particulier...1h20...
Pourriez-vous être plus précis en m'indiquant à quelle minute le sujet en question est abordé ?
Merci
Mathieu
_______________________________________
"Tout envisager, ne rien croire" Aimé Michel
 NycolasEquipe du forum
NycolasEquipe du forum

 Age : 51
Age : 51
Nombre de messages : 716
Inscription : 30/12/2009
Localisation : Saint-Etienne
Emploi : Ecrivain
Passions : Ecriture...
Règlement : Règlement
Points de Participation : 6895
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mer 26 Nov 2014, 16:31
Bon, j'ai retrouvé le passage qui me pose un doute. C'est grosso modo entre 34 minutes et 36 minutes 30, où JPP parle de torpilles à effet MHD produites aux USA.
 Painde2Equipe du forum
Painde2Equipe du forum

 Age : 54
Age : 54
Nombre de messages : 367
Inscription : 25/06/2012
Localisation : Lorient
Emploi : Contrôleur de travaux finis
Passions : Kinderophiliste
Règlement : Règlement
Points de Participation : 4980
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mer 26 Nov 2014, 17:41
Bonsoir à tous
Je me rends compte que le Cas C de mes petits dessins représente par exemple la lune (bille magique) gravitant autour de la terre (la boule).
Je n’ai fait que représenter la courbure de mon drap avec au milieu la boule de pétanque que j’y ai placé et la bille en acier que je m’amuse à lancer. Le résultat est, qu’avec ces déformations, la trajectoire de la bille est courbée. Il y a 2 creux gravitationnels qui ne s’annulent pas.
J’arrive, avec difficultés, à modifier cette courbure de la trajectoire en plaçant un doigt sous le drap, juste sous la bille (il faut être très rapide et précis). Comme je n’y arrivais pas très bien, j’ai placé un tasseau de bois sous le drap pour annuler la déformation de la boule. Résultat : J’arrive à obtenir une trajectoire linéaire si je lance ma bille au dessus du tasseau. J’ai simulé l’annulation de l’effet de gravité et je rejoins ce que vous dites Nycolas.
Par contre je n’arrive pas à représenter un effet de répulsion sauf si mon doigt est légèrement décalé par rapport à la bille. Je crois comprendre dans l’article que la déformation gravitationnelle envisagée, s’effectue uniquement ou la bille se trouve… La, je sèche.
A+

Je me rends compte que le Cas C de mes petits dessins représente par exemple la lune (bille magique) gravitant autour de la terre (la boule).
Je n’ai fait que représenter la courbure de mon drap avec au milieu la boule de pétanque que j’y ai placé et la bille en acier que je m’amuse à lancer. Le résultat est, qu’avec ces déformations, la trajectoire de la bille est courbée. Il y a 2 creux gravitationnels qui ne s’annulent pas.
J’arrive, avec difficultés, à modifier cette courbure de la trajectoire en plaçant un doigt sous le drap, juste sous la bille (il faut être très rapide et précis). Comme je n’y arrivais pas très bien, j’ai placé un tasseau de bois sous le drap pour annuler la déformation de la boule. Résultat : J’arrive à obtenir une trajectoire linéaire si je lance ma bille au dessus du tasseau. J’ai simulé l’annulation de l’effet de gravité et je rejoins ce que vous dites Nycolas.
Par contre je n’arrive pas à représenter un effet de répulsion sauf si mon doigt est légèrement décalé par rapport à la bille. Je crois comprendre dans l’article que la déformation gravitationnelle envisagée, s’effectue uniquement ou la bille se trouve… La, je sèche.
A+

 NycolasEquipe du forum
NycolasEquipe du forum

 Age : 51
Age : 51
Nombre de messages : 716
Inscription : 30/12/2009
Localisation : Saint-Etienne
Emploi : Ecrivain
Passions : Ecriture...
Règlement : Règlement
Points de Participation : 6895
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mer 26 Nov 2014, 17:58
Je crois vraiment que l'analogie du drap risque de nous induire en erreur, même si je salue votre tentative. On pourrait avec ça parvenir à simuler quelques trucs, mais ça reste plutôt artificiel. Je n'en ai pas de meilleure cependant, et j'ai tendance à davantage raisonner dans l'abstrait qu'avec l'aide d'analogies qui ont toujours leurs biais. Je ne dis pas qu'il ne faut pas essayer.
Pour l'effet de répulsion, cela implique que l'effet anti-gravitationnel est produit en réaction à l'objet produisant la gravitation la plus forte (ici, la Terre), ce qui pourrait être représenté par un vecteur de force opposé à celui engendré par la Terre. J'ai du mal à voir comment on peut représenter cela à partir d'un drap : il faudrait que, localement, la bille satellite, crée une force gravitationnelle opposée et d'intensité supérieure (sans quoi il n'y aurait pas répulsion). De telle manière qu'au lieu de rouler vers la Terre, elle roule ailleurs. Vous faites cela en déplaçant la dépression inversée en avant de la bille, ce qui est logique, mais n'est pas conforme à l'hypothèse : c'est plutôt un trucage ad hoc.
Je comprends bien que cela permets de reproduire l'effet d'aspiration anti-gravitationnelle (vers le haut) de l'avion mentionné dans le cas, cependant. Vraisemblablement (si l'on prend le cas de cette façon là), il y a une bulle, un champ, qui dépasse la taille de la bille satellite. Je sais que ce que je dis ne nous avance pas beaucoup pour modéliser la chose, mais je bute sur l'analogie du drap. Je pense toujours à des vecteurs de force : soit il y a un vecteur opposé, soit il y a annulation locale du vecteur de gravité, par un moyen ou par un autre. Autrement dit, la gravitation ne passe pas par ce champ. Et alors on tombe sur une autre possibilité qui est que, localement, le drap est "plat" (annulation de la gravité), voire incliné dans le sens opposé à la pente de la gravitation représentée par le drap (répulsion). Mais est-ce que cela répond au problème du champ ? Peut-être, si cette zone d'inclinaison divergente est étendue autour de la bille.
Bon, je réfléchis à voix haute, là.
Pour l'effet de répulsion, cela implique que l'effet anti-gravitationnel est produit en réaction à l'objet produisant la gravitation la plus forte (ici, la Terre), ce qui pourrait être représenté par un vecteur de force opposé à celui engendré par la Terre. J'ai du mal à voir comment on peut représenter cela à partir d'un drap : il faudrait que, localement, la bille satellite, crée une force gravitationnelle opposée et d'intensité supérieure (sans quoi il n'y aurait pas répulsion). De telle manière qu'au lieu de rouler vers la Terre, elle roule ailleurs. Vous faites cela en déplaçant la dépression inversée en avant de la bille, ce qui est logique, mais n'est pas conforme à l'hypothèse : c'est plutôt un trucage ad hoc.
Je comprends bien que cela permets de reproduire l'effet d'aspiration anti-gravitationnelle (vers le haut) de l'avion mentionné dans le cas, cependant. Vraisemblablement (si l'on prend le cas de cette façon là), il y a une bulle, un champ, qui dépasse la taille de la bille satellite. Je sais que ce que je dis ne nous avance pas beaucoup pour modéliser la chose, mais je bute sur l'analogie du drap. Je pense toujours à des vecteurs de force : soit il y a un vecteur opposé, soit il y a annulation locale du vecteur de gravité, par un moyen ou par un autre. Autrement dit, la gravitation ne passe pas par ce champ. Et alors on tombe sur une autre possibilité qui est que, localement, le drap est "plat" (annulation de la gravité), voire incliné dans le sens opposé à la pente de la gravitation représentée par le drap (répulsion). Mais est-ce que cela répond au problème du champ ? Peut-être, si cette zone d'inclinaison divergente est étendue autour de la bille.
Bon, je réfléchis à voix haute, là.
 InvitéInvité
InvitéInvité
 Re: Contrôle local de la gravitation
Re: Contrôle local de la gravitation
Mer 26 Nov 2014, 20:05
Bonsoir Painde2
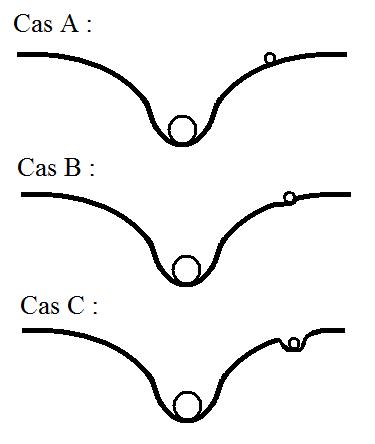
La bille a une masse, elle déforme donc l'espace-temps en collaboration avec la masse de la boule de pétanque.
Il est donc nécessaire pour connaître la déformation réelle de faire la somme point à point des déformations amenées par les deux éléments pris séparément.
Evidemment le "trou" causé par la bille est plus complexe avec la présence de la boule de pétanque mais il est facile de démontrer qu"en aucun cas la bille ne peut rester "coincée" dans le trou qu'elle provoque. Quel que soit le cas envisagé elle finit toujours pas rejoindre la boule de pétanque.
Exemple simplifié :

Bonne soirée.
...

La bille a une masse, elle déforme donc l'espace-temps en collaboration avec la masse de la boule de pétanque.
Il est donc nécessaire pour connaître la déformation réelle de faire la somme point à point des déformations amenées par les deux éléments pris séparément.
Evidemment le "trou" causé par la bille est plus complexe avec la présence de la boule de pétanque mais il est facile de démontrer qu"en aucun cas la bille ne peut rester "coincée" dans le trou qu'elle provoque. Quel que soit le cas envisagé elle finit toujours pas rejoindre la boule de pétanque.
Exemple simplifié :

Bonne soirée.
...
Page 2 sur 5 •  1, 2, 3, 4, 5
1, 2, 3, 4, 5 
 1, 2, 3, 4, 5
1, 2, 3, 4, 5 
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Témoigner
Témoigner 
